El **mapa de Karnaugh de 3 variables** es una herramienta esencial para simplificar expresiones booleanas y, por ende, optimizar el diseño de circuitos digitales. Esta técnica gráfica, intuitiva y visual, permite agrupar términos adyacentes en el mapa para obtener una expresión mínima equivalente, lo que se traduce en una reducción de la complejidad del circuito y un menor consumo de energía.
Lectura Rápida
- Representación gráfica de funciones booleanas.
- Simplifica expresiones algebraicas complejas.
- Utiliza un diagrama de 2 dimensiones.
- Organiza minitérminos en celdas adyacentes.
- Grupos de celdas representan términos simplificados.
- Identifica grupos de 1, 2, 4 u 8 celdas.
- Minimiza el número de compuertas lógicas.
- Mejora la eficiencia y el rendimiento de los circuitos.
El Mapa de Karnaugh de 3 Variables: Una Herramienta Esencial en la Simplificación de Circuitos Digitales
En el mundo de la electrónica digital, la optimización de los circuitos es una tarea crucial. Para lograrla, se emplean diversas herramientas, entre las que destaca el mapa de Karnaugh de 3 variables. Este método gráfico se ha convertido en un aliado fundamental para simplificar las funciones booleanas y obtener diseños de circuitos más eficientes y compactos.
Presenta una estructura de 2×4 para representar las variables de entrada
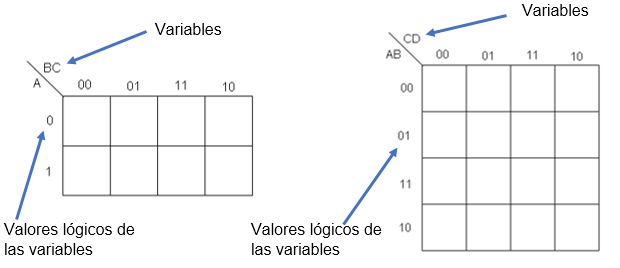
El mapa de Karnaugh de 3 variables se caracteriza por su estructura de 2×4, donde cada celda representa una combinación única de las variables de entrada. Se utilizan tres variables, comúnmente denominadas A, B y C, cada una con dos posibles valores: 0 o 1. La disposición de las celdas en el mapa se basa en el código Gray, que asegura que solo un bit cambia entre celdas adyacentes.
| ABC | 0 | 1 |
| 00 | 000 | 001 |
| 01 | 011 | 010 |
| 11 | 110 | 111 |
| 10 | 101 | 100 |
Este mapa nos ayuda a visualizar las diferentes combinaciones posibles de las variables de entrada.
Agrupa las celdas que representan un valor 1
El siguiente paso consiste en asignar a cada celda un valor de 0 o 1, dependiendo de la función booleana que se desea simplificar. Las celdas con valor 1 representan las combinaciones de entrada que producen una salida de 1. Una vez que el mapa está lleno, se procede a agrupar las celdas adyacentes que contienen un valor 1. Estas agrupaciones deben ser rectangulares y de tamaño potencia de 2 (1, 2, 4, 8, etc.). Cada agrupación representa un término de la expresión booleana simplificada.
Por ejemplo, si tenemos un mapa de Karnaugh con las siguientes combinaciones de entrada que producen un valor 1: 000, 001, 011 y 111, se pueden agrupar de la siguiente manera:
- Agrupación 1: Celdas 000 y 001 (representan el término A’B’C)
- Agrupación 2: Celdas 011 y 111 (representan el término B’C)
Aplicaciones Prácticas del Mapa de Karnaugh de 3 Variables
El mapa de Karnaugh 3 variables tiene un amplio rango de aplicaciones prácticas en el diseño de circuitos digitales. Su utilidad se extiende desde la simplificación de la lógica de los sistemas de control hasta la optimización del diseño de circuitos combinacionales.
Simplifica la lógica de los sistemas de control
En los sistemas de control, el mapa de Karnaugh juega un papel esencial en la simplificación de las expresiones booleanas que rigen el funcionamiento del sistema. Permite optimizar la lógica de control, reduciendo la cantidad de compuertas lógicas necesarias y facilitando el análisis y la implementación del sistema.
Optimiza el diseño de circuitos combinacionales
Los circuitos combinacionales son aquellos cuya salida depende únicamente de sus entradas actuales, sin memoria de estados anteriores. En estos circuitos, el mapa de Karnaugh 3 variables se usa para simplificar las funciones booleanas que determinan la salida del circuito. Esto conduce a un diseño más eficiente, con menor cantidad de componentes y un funcionamiento más rápido y eficiente.
Pasos para Construir un Mapa de Karnaugh de 3 Variables
Construir un mapa de Karnaugh 3 variables es un proceso sencillo que se realiza en tres pasos:
Lee También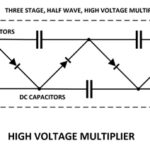
Multiplicador de Voltaje AC: Aumenta la Tensión con Circuitos SimplesDefinir las variables de entrada y la función de salida
El primer paso consiste en identificar las variables de entrada que influyen en la salida del circuito. Se define el nombre de cada variable (A, B, C) y el rango de valores que puede tomar (generalmente 0 y 1). Luego se define la función de salida, que representa la operación lógica que se realiza con las variables de entrada.
Asignar los valores binarios a las variables de entrada
En el siguiente paso, se asignan los valores binarios a cada combinación de las variables de entrada. Se utiliza el código Gray para garantizar que solo un bit cambie entre celdas adyacentes.
Llenar el mapa de Karnaugh con los valores de la función de salida
Finalmente, se completa el mapa de Karnaugh con los valores de la función de salida para cada combinación de entrada.
Ventajas del Mapa de Karnaugh en el Diseño de Circuitos Digitales
El mapa de Karnaugh de 3 variables ofrece diversas ventajas en el diseño de circuitos digitales:
Reduce la complejidad de los circuitos
Al simplificar las funciones booleanas, el mapa de Karnaugh 3 variables reduce el número de compuertas lógicas necesarias para implementar el circuito. Esto se traduce en un diseño más sencillo y económico, con menor cantidad de componentes y conexiones.
Optimiza el uso de compuertas lógicas
La simplificación de las funciones booleanas permite un uso más eficiente de las compuertas lógicas. Se minimiza el número de compuertas y se optimiza la combinación de ellas, lo que conduce a un circuito más compacto y de menor consumo de energía.
Facilita la comprensión de la lógica del circuito
El mapa de Karnaugh 3 variables proporciona una representación gráfica sencilla de las variables y sus valores. Esto facilita la comprensión de la lógica del circuito y su comportamiento, lo que es especialmente útil para el análisis y depuración del circuito.
Ejemplos de Aplicaciones del Mapa de Karnaugh de 3 Variables
El mapa de Karnaugh de 3 variables se aplica en una gran variedad de circuitos digitales, entre ellos:
Diseño de un decodificador de 3 bits
Un decodificador de 3 bits convierte un código binario de 3 bits en una señal única que corresponde a la combinación de entrada. El mapa de Karnaugh 3 variables se puede utilizar para simplificar la lógica del decodificador, reduciendo el número de compuertas lógicas necesarias.
Simplificación de un circuito sumador de 3 bits
Un circuito sumador de 3 bits suma dos números binarios de 3 bits, produciendo un resultado de 4 bits. El mapa de Karnaugh 3 variables se utiliza para simplificar las funciones booleanas que rigen la suma de los bits, lo que optimiza el diseño del circuito y lo hace más eficiente.
Lee También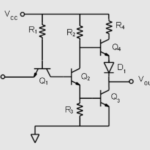
Niveles Lógicos de Voltaje: Guía Completa para Electrónica DigitalLimitaciones del Mapa de Karnaugh de 3 Variables
A pesar de sus ventajas, el mapa de Karnaugh de 3 variables presenta algunas limitaciones:
Efectividad limitada para funciones con un alto número de variables
La complejidad del mapa de Karnaugh aumenta rápidamente con el número de variables de entrada. Para funciones con más de 4 variables, su uso se vuelve poco práctico debido a la dificultad de visualizar y agrupar las celdas.
Dificultad para tratar funciones con múltiples salidas
El mapa de Karnaugh está diseñado para tratar funciones con una sola salida. Para funciones con múltiples salidas, se requiere construir un mapa independiente para cada salida, lo que aumenta la complejidad del proceso.
Alternativas al Mapa de Karnaugh para funciones complejas
Para funciones booleanas con un alto número de variables o múltiples salidas, existen alternativas al mapa de Karnaugh 3 variables que permiten simplificar las funciones:
El Álgebra Booleana
El Álgebra Booleana es un sistema matemático que se utiliza para analizar y simplificar funciones booleanas. Se basa en un conjunto de axiomas y teoremas que permiten manipular expresiones booleanas y encontrar soluciones óptimas.
El Método de Quine-McCluskey
El Método de Quine-McCluskey es un algoritmo que permite simplificar funciones booleanas mediante la eliminación de términos redundantes. Se basa en la comparación de los términos de la función para identificar aquellos que pueden ser combinados en términos más simples.
El Método de Tablas de Verdad
El Método de Tablas de Verdad es una técnica que se utiliza para representar las funciones booleanas mediante una tabla. Cada fila de la tabla representa una combinación de las variables de entrada, y cada columna representa la salida de la función para esa combinación.
En conclusión, el mapa de Karnaugh 3 variables es una herramienta fundamental en el diseño de circuitos digitales, especialmente para simplificar funciones booleanas con un número limitado de variables. Su aplicación en la optimización del diseño de circuitos combinacionales y la simplificación de la lógica de los sistemas de control lo convierte en un recurso invaluable para diseñadores electrónicos.
Sin embargo, para funciones más complejas con un alto número de variables o múltiples salidas, es necesario recurrir a alternativas como el Álgebra Booleana, el Método de Quine-McCluskey o el Método de Tablas de Verdad.
Video sobre Mapa Karnaugh 3 Variables: Simplifica Circuitos Digitales
Preguntas Frecuentes
¿Cómo se representa una función booleana de 3 variables en un mapa de Karnaugh?
Para representar una función booleana de 3 variables en un mapa de Karnaugh, se utiliza una cuadrícula de 2×4 celdas. Cada celda corresponde a una única combinación de las tres variables de entrada, A, B y C. Las filas del mapa representan las combinaciones de las variables A y B, mientras que las columnas representan las combinaciones de la variable C.
Lee También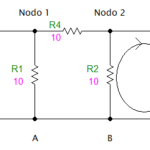
Nodo Eléctrico: Qué es y su Importancia en la ElectrónicaLas celdas se llenan con el valor de la función booleana para la combinación de entrada que representa cada celda. Por ejemplo, si la función booleana es F(A, B, C) = A’BC + AB’C + ABC’, la celda correspondiente a la combinación de entrada A=0, B=1, C=1 tendrá un valor de 1, ya que la función booleana se evalúa como 1 para esta combinación de entrada.
¿Qué son los grupos adyacentes en un mapa de Karnaugh y cómo se identifican?
En un mapa de Karnaugh, los grupos adyacentes son conjuntos de celdas que representan combinaciones de entrada que se diferencian en un solo bit. Estas celdas se agrupan para simplificar la función booleana, ya que cada grupo representa un término de la expresión simplificada.
Los grupos adyacentes se identifican buscando celdas que compartan un lado común. Es importante destacar que las celdas de los extremos del mapa también pueden ser adyacentes, ya que el mapa se considera como un toro, es decir, las celdas de los extremos se encuentran conectadas. Por ejemplo, la celda 000 puede ser adyacente a la celda 100.
¿Cómo se simplifica una función booleana usando el mapa de Karnaugh?
La simplificación de una función booleana usando el mapa de Karnaugh se realiza mediante la identificación y agrupación de las celdas que representan los valores 1 en el mapa. Cada grupo de celdas adyacentes representa un término de la expresión booleana simplificada.
Se buscan los grupos más grandes posibles, siempre que sean de tamaño potencia de 2 (1, 2, 4, 8, etc.). Los grupos se identifican buscando celdas que compartan un lado común, incluyendo las celdas de los extremos del mapa. Una vez identificados los grupos, se escribe el término correspondiente a cada grupo, y la expresión simplificada se obtiene al sumar los términos de todos los grupos.
¿Cuál es la utilidad del mapa de Karnaugh en la simplificación de circuitos digitales?
El mapa de Karnaugh es una herramienta invaluable en la simplificación de circuitos digitales. Permite visualizar las relaciones entre las variables de entrada y la salida del circuito, lo que facilita la identificación de términos redundantes y la optimización de la expresión booleana.
Al simplificar la expresión booleana, el mapa de Karnaugh permite reducir el número de compuertas lógicas necesarias para implementar el circuito. Esto se traduce en un diseño más eficiente, con menor cantidad de componentes, conexiones y un consumo de energía más bajo. Además, la simplificación facilita la comprensión de la lógica del circuito y su comportamiento, lo que facilita la depuración y el análisis.
¿Existen limitaciones en el uso del mapa de Karnaugh?
Si bien el mapa de Karnaugh es una herramienta poderosa para la simplificación de funciones booleanas, existen limitaciones que debemos considerar. Una de las principales limitaciones es que su uso se vuelve poco práctico para funciones con un alto número de variables.
La complejidad del mapa aumenta rápidamente con el número de variables, lo que dificulta la visualización y la agrupación de celdas. Para funciones con más de 4 variables, es necesario recurrir a otros métodos de simplificación, como el método de Quine-McCluskey o el álgebra booleana.
Concluyendo
El mapa de Karnaugh de 3 variables es un instrumento indispensable en el arte de la simplificación de circuitos digitales. Su estructura de 2×4, que representa cada combinación de variables de entrada, facilita la agrupación de términos y la obtención de expresiones booleanas más concisas y eficientes. Esta herramienta se convierte en un aliado fundamental para optimizar el diseño de circuitos, reducir la complejidad y el consumo energético, y facilitar la comprensión de la lógica del sistema. Sin embargo, para funciones más complejas, el mapa de Karnaugh puede verse limitado, requiriendo la utilización de métodos alternativos como el álgebra booleana o el método de Quine-McCluskey.
Lee También
Simplifica circuitos con mapas de Karnaugh de 2 variablesCompartelo
¿Te has enfrentado a la complejidad de los circuitos digitales? El mapa de Karnaugh de 3 variables te ofrece una solución gráfica y eficiente para simplificar funciones booleanas y optimizar tus diseños. ¡Descubre cómo esta herramienta esencial puede revolucionar tu trabajo!
Comparte este artículo con tus compañeros de ingeniería y déjate llevar por la magia de la simplificación con el mapa de Karnaugh.
