
El sistema binario, también conocido como sistema de numeración binario, es la base de la informática moderna. Este sistema de numeración utiliza solo dos dígitos, el 0 y el 1, para representar cualquier número. La comprensión del sistema binario es fundamental para comprender cómo funcionan las computadoras y otros dispositivos digitales.
- Resumen Clave
- El Sistema Binario: Un Sistema de Numeración Fundamental
- Conversión entre Sistemas Numéricos
- Operaciones Básicas en el Sistema Binario
- + 110
- - 101
- x 11
- +101
- El Lenguaje Binario: Codificando Información
- Aplicaciones del Sistema Binario
- Historia del Sistema Binario
- Video sobre Tabla Binaria: Sistema de Numeración Binario y Lenguaje Binario
- Preguntas Frecuentes
- Conclusión
- Compartelo
Resumen Clave
- El sistema binario utiliza solo dos dígitos (0 y 1) para representar números, en contraste con el sistema decimal que emplea diez.
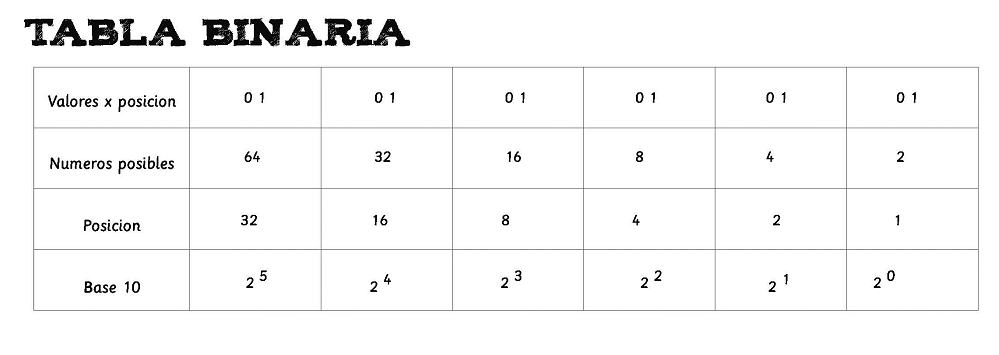
- Cada posición en un número binario representa una potencia de dos, comenzando desde 2 elevado a la potencia 0 en la posición derecha.
- El sistema binario es fundamental para la informática, ya que las computadoras procesan información en forma de 0s y 1s.
- Convertir un número decimal a binario implica dividir el número decimal por dos repetidamente y registrar el residuo (0 o 1).
- Los números binarios se utilizan para representar diferentes tipos de información, incluyendo datos, instrucciones y códigos.
- Una tabla binaria facilita la conversión entre números decimales y binarios al mostrar la equivalencia de cada posición.
- El sistema binario es una forma eficiente de representar información digital, debido a su simplicidad y capacidad de ser fácilmente procesada por las computadoras.
El Sistema Binario: Un Sistema de Numeración Fundamental
El Sistema Binario: Un Sistema de Numeración Basado en Dos Dígitos
El sistema binario, también conocido como sistema de numeración binaria, es un sistema de numeración que solo utiliza dos dígitos: 0 y 1. Este sistema es la base de la informática y la electrónica moderna, ya que las computadoras trabajan con estados de encendido y apagado, representados por 1 y 0 respectivamente. En el sistema binario, cada posición de un número representa una potencia de dos, empezando por 2⁰ (que es igual a 1) en la posición de las unidades.
Por ejemplo, el número decimal 5 se representa en binario como 101, ya que:
- 1 × 2² = 4
- 0 × 2¹ = 0
- 1 × 2⁰ = 1
En el sistema decimal, cada posición de un número representa una potencia de diez. Por ejemplo, el número decimal 123 se representa como:
- 1 × 10² = 100
- 2 × 10¹ = 20
- 3 × 10⁰ = 3
El Sistema Binario en la Informática y la Electrónica
El sistema binario es fundamental en la informática y la electrónica, ya que permite representar la información de manera sencilla y eficiente. Las computadoras utilizan circuitos electrónicos que trabajan con dos estados: encendido (1) y apagado (0). Estos estados se representan con bits, que son la unidad básica de información en la informática.
Un bit puede representar dos valores, 0 o 1, y se utiliza para almacenar información en la memoria de una computadora. Las computadoras utilizan combinaciones de bits para representar letras, números, imágenes, sonido y otros tipos de datos.
Conversión entre Sistemas Numéricos
Conversión de Decimal a Binario
Para convertir un número decimal a binario, se divide el número decimal por 2 y se anota el resto de la división. Luego, se divide el cociente por 2 nuevamente y se anota el resto, y así sucesivamente hasta que el cociente sea 0. Los restos, escritos en orden inverso, forman el número binario.
Ejemplo: Convierte el número decimal 13 a binario.
- 13 / 2 = 6 (resto 1)
- 6 / 2 = 3 (resto 0)
- 3 / 2 = 1 (resto 1)
- 1 / 2 = 0 (resto 1)
El número binario es 1101, formado por los restos en orden inverso.
Conversión de Binario a Decimal
Para convertir un número binario a decimal, se multiplica cada dígito del número binario por la correspondiente potencia de 2, empezando por 2⁰ (que es igual a 1) en la posición de las unidades. Luego, se suman los productos obtenidos.
Lee También Fórmulas de MRU: Cómo Calcular el Movimiento Rectilíneo Uniforme
Fórmulas de MRU: Cómo Calcular el Movimiento Rectilíneo UniformeEjemplo: Convierte el número binario 1011 a decimal.
- 1 × 2³ = 8
- 0 × 2² = 0
- 1 × 2¹ = 2
- 1 × 2⁰ = 1
El número decimal es 8 + 0 + 2 + 1 = 11.
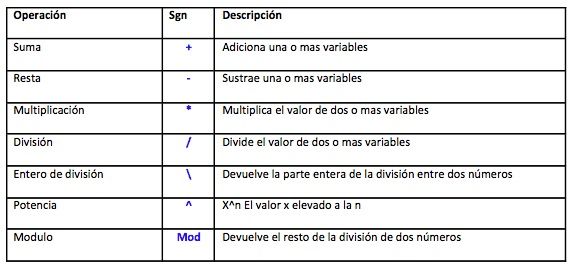
Operaciones Básicas en el Sistema Binario
Suma en Binario
Para sumar dos números binarios, se suma cada columna de dígitos, teniendo en cuenta que:
- 0 + 0 = 0
- 0 + 1 = 1
- 1 + 0 = 1
- 1 + 1 = 0 (con acarreo de 1 a la columna siguiente)
Ejemplo: Suma los números binarios 101 y 110.
```
101
+ 110
1011
```
- La suma de la columna de las unidades es 1 + 0 = 1.
- La suma de la columna siguiente es 0 + 1 = 1.
- La suma de la columna siguiente es 1 + 1 = 0 (con acarreo de 1).
- El acarreo se suma a la siguiente columna, que queda como 1.
El resultado de la suma es 1011.
Resta en Binario
Para restar dos números binarios, se resta cada columna de dígitos, teniendo en cuenta que:
- 0 - 0 = 0
- 1 - 0 = 1
- 1 - 1 = 0
- 0 - 1 = 1 (con préstamo de 1 de la columna siguiente)
Ejemplo: Resta el número binario 101 de 110.
```
110
- 101
001
```
- La resta de la columna de las unidades es 0 - 1 = 1 (con préstamo de 1).
- El préstamo se resta de la siguiente columna, que queda como 0 - 1 = 1 (con préstamo de 1).
- El préstamo se resta de la siguiente columna, que queda como 1 - 1 = 0.
El resultado de la resta es 001.
Multiplicación en Binario
Para multiplicar dos números binarios, se multiplica cada dígito del multiplicando por cada dígito del multiplicador, sumando los productos parciales. La multiplicación binaria se basa en la suma binaria.
Ejemplo: Multiplica los números binarios 101 y 11.
```
101
x 11
101
+101
1111
```
- 1 × 101 = 101
- 1 × 101 = 101
- Se suman los productos parciales, teniendo en cuenta que la segunda línea se desplaza un lugar a la izquierda.
El resultado de la multiplicación es 1111.
División en Binario
Para dividir dos números binarios, se divide el dividendo por el divisor, utilizando el algoritmo de la división. La división binaria se basa en la resta binaria.
Ejemplo: Divide el número binario 110 por 10.
Lee TambiénSumas y Restas Horizontales: Un Método Sencillo y Eficaz
10 | 110
|----
10
----
10
----
0
- Se divide el primer dígito del dividendo (1) por el divisor (10). Como el divisor es mayor que el dividendo, se baja el siguiente dígito (1) formando 11.
- Se divide 11 por 10, obteniendo un cociente de 1 y un resto de 1. Se escribe el cociente (1) y se baja el último dígito (0) del dividendo, formando 10.
- Se divide 10 por 10, obteniendo un cociente de 1 y un resto de 0. Se escribe el cociente (1) y el resto (0).
El resultado de la división es 11 con un resto de 0.
El Lenguaje Binario: Codificando Información
El Lenguaje Binario: Un Código Basado en Bits
El lenguaje binario es un código que utiliza secuencias de bits (dígitos binarios) para representar letras, números y símbolos. Cada carácter, como una letra, un número o un símbolo, se representa mediante una combinación única de bits.
Por ejemplo, la letra A se representa como 01000001 en el código ASCII (American Standard Code for Information Interchange). El código ASCII utiliza 7 bits para representar cada carácter, lo que permite representar 128 caracteres diferentes.
Códigos ASCII y Unicode: Estándares para la Codificación de Texto
El código ASCII es un estándar de codificación de caracteres que se utiliza para representar caracteres en computadoras y dispositivos de comunicación. Sin embargo, el código ASCII solo permite representar 128 caracteres, lo que no es suficiente para representar todos los caracteres de todos los idiomas del mundo.
El estándar Unicode es una extensión del código ASCII que permite representar más de 100,000 caracteres, incluyendo caracteres de todos los idiomas del mundo. Unicode utiliza 16 bits para representar cada carácter, lo que permite representar 65,536 caracteres diferentes.
La importancia de los códigos ASCII y Unicode radica en que permiten a las computadoras y dispositivos de comunicación entenderse entre sí, independientemente del idioma o la plataforma utilizada.
Aplicaciones del Sistema Binario
El Sistema Binario en la Electrónica Digital
El sistema binario se utiliza en la electrónica digital para representar estados de encendido y apagado. Los circuitos digitales utilizan transistores que actúan como interruptores, permitiendo o bloqueando el flujo de corriente. El estado de encendido se representa con un 1 y el estado de apagado con un 0.
Las computadoras utilizan circuitos digitales para procesar información y realizar cálculos. Los bits se utilizan para representar datos en la memoria de la computadora, y los circuitos digitales se utilizan para realizar operaciones matemáticas y lógicas con los datos.
El Sistema Binario en la Informática
El sistema binario es fundamental en la informática, ya que permite representar la información de manera eficiente y compacta. Las computadoras utilizan bits para representar datos, instrucciones, direcciones de memoria y otros tipos de información.
Lee También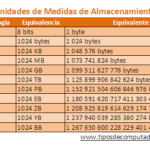 Unidades de Información: Bit, Byte, Hertz y Bits por Segundo
Unidades de Información: Bit, Byte, Hertz y Bits por SegundoEl lenguaje binario se utiliza para comunicar instrucciones a la computadora, y el código máquina se utiliza para traducir el código fuente de los programas a lenguaje binario.
Historia del Sistema Binario
El Sistema Binario en la Antigua China
El sistema binario se conoce desde la antigua China, donde se utilizó para representar los números con el sistema de numeración binario. El libro I Ching, un texto chino clásico sobre filosofía y adivinación, utiliza una serie de líneas continuas y discontinuas para representar los números binarios.
El Sistema Binario en la Era Moderna
En la era moderna, el sistema binario fue desarrollado por Gottfried Wilhelm Leibniz, un matemático y filósofo alemán, en el siglo XVII. Leibniz desarrolló un sistema de numeración binario que utiliza 0 y 1 para representar todos los números.
La Importancia de Claude Shannon en el Desarrollo del Sistema Binario
Claude Shannon, un ingeniero e informático estadounidense, publicó en 1938 un artículo titulado "A Symbolic Analysis of Relay and Switching Circuits", que estableció los fundamentos de la teoría de la información y la lógica digital. En este artículo, Shannon demostró que los circuitos digitales pueden utilizarse para representar información y realizar operaciones lógicas utilizando el sistema binario.
La investigación de Shannon fue fundamental para el desarrollo de la informática moderna, ya que permitió construir computadoras y dispositivos digitales basados en el sistema binario.
La importancia de Claude Shannon en el desarrollo del sistema binario radica en que fue el primero en demostrar la posibilidad de utilizar los circuitos digitales para representar información y realizar operaciones lógicas utilizando el sistema binario. Su trabajo sentó las bases para el desarrollo de la informática moderna.
En el amor y las relaciones, el número 000 representa un mensaje de amor incondicional y posibilidades infinitas. Refleja la idea de la totalidad y la unión de dos almas que se convierten en una. Te anima a ver la belleza en tu pareja y a apreciarla por quien es. Significa la importancia del amor, la comunicación y la unidad en cualquier relación.
El sistema binario es un sistema de numeración fundamental en la informática y la electrónica moderna. Su simplicidad y eficiencia lo convierten en la base de la comunicación entre las computadoras y dispositivos digitales. El lenguaje binario, que utiliza secuencias de bits para representar información, es fundamental para el funcionamiento de la tecnología moderna.
El sistema binario ha permitido el desarrollo de computadoras y dispositivos digitales que han revolucionado la vida moderna. Gracias a su versatilidad y eficiencia, el sistema binario continuará siendo fundamental para la innovación tecnológica en los próximos años.
Video sobre Tabla Binaria: Sistema de Numeración Binario y Lenguaje Binario
Preguntas Frecuentes
¿Cómo puedo convertir un número decimal a binario?
Para convertir un número decimal a binario, se utiliza un proceso iterativo de divisiones sucesivas por 2. Se divide el número decimal por 2 y se anota el resto de la división. Luego, se divide el cociente por 2 nuevamente y se anota el resto, y así sucesivamente hasta que el cociente sea 0. Los restos, escritos en orden inverso, forman el número binario.
Lee TambiénPor ejemplo, para convertir el número decimal 13 a binario:
1. 13 / 2 = 6 (resto 1)
2. 6 / 2 = 3 (resto 0)
3. 3 / 2 = 1 (resto 1)
4. 1 / 2 = 0 (resto 1)
El número binario es 1101, formado por los restos en orden inverso.
¿Qué significa el 0 y el 1 en el sistema binario?
En el sistema binario, el 0 y el 1 representan dos estados opuestos. En el ámbito de la informática y la electrónica, se suele asociar el 0 al estado de apagado (sin corriente) y el 1 al estado de encendido (con corriente).
Estos dos dígitos, combinados en secuencias, permiten representar cualquier número, letra o símbolo en el mundo digital. Un solo bit (0 o 1) puede almacenar una pequeña cantidad de información, pero al combinarse en cadenas, se pueden crear estructuras de datos complejas y almacenar grandes cantidades de información.
¿Cuál es la diferencia entre el código ASCII y Unicode?
El código ASCII (American Standard Code for Information Interchange) es un estándar de codificación de caracteres que utiliza 7 bits para representar cada carácter, lo que permite representar 128 caracteres diferentes. Sin embargo, este estándar no es suficiente para representar todos los caracteres de todos los idiomas del mundo.
Unicode, por otro lado, es una extensión del código ASCII que utiliza 16 bits para representar cada carácter, lo que permite representar más de 100,000 caracteres, incluyendo caracteres de todos los idiomas del mundo.
ASCII es un sistema de codificación más antiguo y limitado, mientras que Unicode es un sistema más moderno y completo que permite representar una mayor variedad de caracteres.
¿Cómo se utiliza el sistema binario en la informática?
El sistema binario es fundamental en la informática ya que permite representar la información de manera eficiente y compacta. Las computadoras utilizan bits para representar datos, instrucciones, direcciones de memoria y otros tipos de información.
Cada bit representa un estado, encendido (1) o apagado (0), que se utiliza para procesar información. Las computadoras trabajan con estos bits como unidades básicas de información, combinándolos en secuencias para crear programas, archivos y datos.
¿Cuáles son algunas de las aplicaciones del sistema binario en la vida real?
El sistema binario tiene una amplia gama de aplicaciones en la vida real, desde los dispositivos que usamos a diario hasta las tecnologías más avanzadas. Por ejemplo, se utiliza en:
- Computadoras y dispositivos digitales: Los circuitos digitales de las computadoras y otros dispositivos digitales se basan en el sistema binario para representar y procesar información.
- Comunicaciones: Las señales digitales, como las que se utilizan en las redes de telefonía móvil o en internet, se transmiten utilizando el sistema binario.
- Sensores y dispositivos electrónicos: Muchos sensores y dispositivos electrónicos utilizan el sistema binario para convertir señales analógicas en señales digitales.
- Imágenes digitales: Las imágenes digitales, como las fotografías o las imágenes de video, se almacenan y procesan utilizando el sistema binario.
el sistema binario es una herramienta fundamental que ha revolucionado la tecnología moderna, permitiendo el desarrollo de una amplia gama de dispositivos y aplicaciones que usamos en la vida diaria.
Conclusión
El sistema binario, un lenguaje de 0 y 1, es la piedra angular de la informática moderna. Desde el encendido y apagado de los circuitos hasta la codificación de la información, este sistema sencillo y potente ha dado forma a nuestra era digital. El sistema binario nos permite comunicar con las máquinas y procesar información a velocidades inimaginables, abriendo un universo de posibilidades que solo se limita por nuestra imaginación.
Compartelo
¿Te has preguntado cómo las computadoras "hablan"? La respuesta está en el sistema binario, un lenguaje que utiliza solo 0 y 1. ¡En este artículo te explicamos todo lo que necesitas saber!
Descubre cómo convertir números decimales a binarios, cómo se usan las operaciones básicas en binario y cómo funciona el lenguaje binario en la comunicación entre humanos y máquinas.
¡Comparte este artículo con tus amigos y ayúdanos a difundir el conocimiento sobre este fascinante sistema!
SistemaBinario #LenguajeBinario #Tecnología #Informática #Ciencia #Educación #Aprendizaje #Computación
Deja una respuesta


También te puede interesar: