Sumérgete en el fascinante mundo de los capacitores, elementos fundamentales en la electrónica. En este viaje, exploraremos la magia de las conexiones en serie y paralelo, desentrañando sus fórmulas y resolviendo ejercicios que iluminarán tu comprensión de estos circuitos. Desvelaremos cómo se comportan los capacitores al unirse en estas configuraciones, descubriendo la clave para calcular la capacitancia equivalente y comprender su comportamiento en circuitos mixtos.
Resumen Clave
- Los capacitores conectados en paralelo suman sus capacitancias para obtener una capacitancia equivalente mayor.
- La fórmula para calcular la capacitancia equivalente en paralelo es: Ceq = C1 + C2 + … + Cn.
- Los capacitores conectados en serie tienen una capacitancia equivalente menor que la del capacitor más pequeño.
- La fórmula para calcular la capacitancia equivalente en serie es: 1/Ceq = 1/C1 + 1/C2 + … + 1/Cn.
- Los circuitos mixtos de capacitores combinan conexiones en serie y paralelo, requiriendo un análisis paso a paso.
- La capacitancia equivalente de un circuito mixto se calcula resolviendo las conexiones en serie y paralelo de forma secuencial.
- Existen ejercicios resueltos que ilustran la aplicación de las fórmulas y la resolución de circuitos mixtos de capacitores.
Capacitores en Serie: Características y Fórmula
Corriente y Carga en Capacitores en Serie
Cuando conectas capacitores en serie, la corriente que circula por cada uno de ellos es la misma. Esto significa que la carga eléctrica (Q) también es la misma para todos los capacitores. ¿Por qué? Porque la corriente debe pasar a través de cada capacitor para llegar al siguiente. Imagina que la corriente es como un río que fluye por un canal. En este caso, el canal está dividido en secciones, cada una representa un capacitor. El agua debe pasar por cada sección para llegar a la siguiente, aunque la cantidad de agua que fluye es la misma en cada sección.
Capacitancia Total en Serie: Fórmula y Relación
La capacitancia total (C) de un circuito en serie se determina mediante la siguiente fórmula:
1/C = 1/C1 + 1/C2 + 1/C3 + ...
Donde:
- C es la capacitancia total
- C1, C2, C3, etc. son las capacitancias de cada capacitor individual
Esta fórmula indica que la capacitancia total en serie es siempre menor que la capacitancia del capacitor más pequeño del circuito. Es como si los capacitores «se opusieran» a la carga total, y la capacitancia total disminuye con la adición de más capacitores en serie.
La relación entre la capacitancia total y la carga eléctrica en un circuito en serie se puede expresar mediante la siguiente fórmula:
Q = C * V
Donde:
Lee También
Capacitores SMD: Guía completa sobre tipos, fallos y cuidados- Q es la carga eléctrica
- C es la capacitancia total
- V es el voltaje aplicado al circuito
Esta fórmula nos permite calcular la carga eléctrica total en un circuito en serie, conociendo la capacitancia total y el voltaje aplicado.
Capacitores en Paralelo: Principios y Fórmula
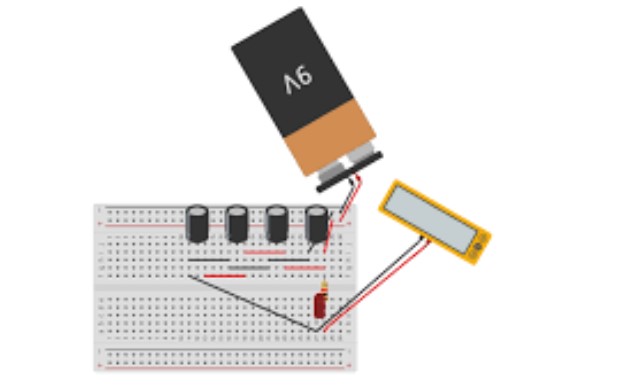
Voltaje en Capacitores en Paralelo
Cuando los capacitores están conectados en paralelo, todos ellos comparten el mismo voltaje. Esto es debido a que todos los capacitores están conectados directamente a la misma fuente de voltaje, como si todos los capacitores estuvieran conectados a un mismo punto.
Capacitancia Total en Paralelo: Suma Directa
La capacitancia total (C) de un circuito en paralelo se calcula simplemente sumando las capacitancias individuales. Es decir, la capacitancia total es la suma de todas las capacitancias individuales.
C = C1 + C2 + C3 + ...
Donde:
- C es la capacitancia total
- C1, C2, C3, etc. son las capacitancias de cada capacitor individual
La capacitancia total en paralelo es siempre mayor que la capacitancia del capacitor más grande. A diferencia de los capacitores en serie, en este caso los capacitores «se complementan» para aumentar la capacitancia total.
Circuitos Mixtos de Capacitores: Combinación Serie-Paralelo
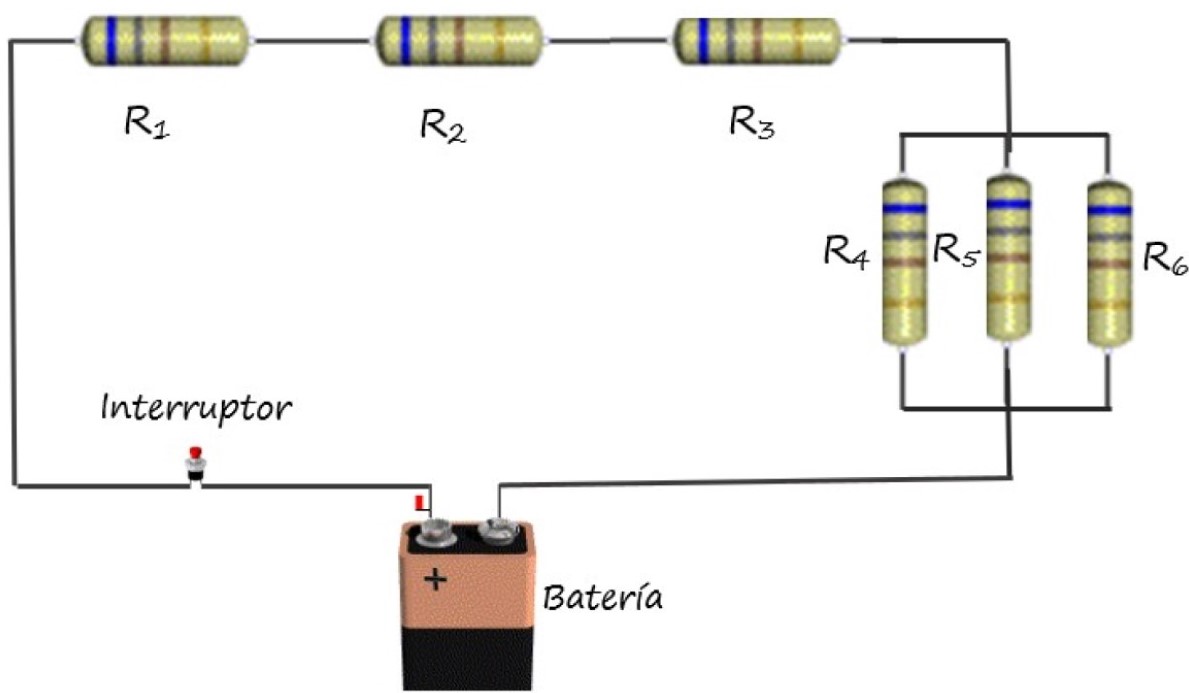
Identificación de Ramas Serie y Paralelo
En un circuito mixto de capacitores, se pueden encontrar combinaciones tanto en serie como en paralelo. Para determinar la capacitancia equivalente del circuito, primero debes identificar las ramas en serie y en paralelo. Imagina un árbol con sus ramas. Cada rama representa una parte del circuito, y las ramas pueden estar conectadas en serie o en paralelo. Para identificar las ramas, observa cómo están conectados los capacitores:
- Serie: Si los capacitores están conectados uno después del otro, formando un solo camino para la corriente, están en serie.
- Paralelo: Si los capacitores están conectados directamente a la misma fuente de voltaje, están en paralelo.
Cálculo de la Capacitancia Equivalente
Una vez que hayas identificado las ramas en serie y en paralelo, puedes calcular la capacitancia equivalente del circuito. Para ello, debes aplicar las fórmulas de capacitancia total para circuitos en serie y en paralelo:
Lee También
Capacitores Variables: Funcionamiento, Tipos, Fallas y Mantenimiento- Calcula la capacitancia equivalente de cada rama en serie.
- Calcula la capacitancia equivalente de cada rama en paralelo.
- Si quedan ramas en serie, vuelve a calcular la capacitancia equivalente.
- Si quedan ramas en paralelo, vuelve a calcular la capacitancia equivalente.
Repite este proceso hasta que obtengas la capacitancia equivalente total del circuito.
Ejemplos de Circuitos con Capacitores
Ejemplos de Capacitores en Serie
- Ejemplo 1: Imagina que tienes dos capacitores, C1 = 10µF y C2 = 20µF, conectados en serie. La capacitancia total se calcula como:
1/C = 1/10µF + 1/20µF = 3/20µF
C = 20µF/3 = 6.67µF
- Ejemplo 2: Si tienes tres capacitores, C1 = 5µF, C2 = 10µF y C3 = 15µF, conectados en serie, la capacitancia total sería:
1/C = 1/5µF + 1/10µF + 1/15µF = 11/30µF
C = 30µF/11 = 2.73µF
Ejemplos de Capacitores en Paralelo
- Ejemplo 1: Si tienes dos capacitores, C1 = 10µF y C2 = 20µF, conectados en paralelo, la capacitancia total sería:
C = C1 + C2 = 10µF + 20µF = 30µF
- Ejemplo 2: Si tienes tres capacitores, C1 = 5µF, C2 = 10µF y C3 = 15µF, conectados en paralelo, la capacitancia total sería:
C = C1 + C2 + C3 = 5µF + 10µF + 15µF = 30µF
Ejemplos de Circuitos Mixtos
- Ejemplo 1: Imagina un circuito con dos ramas: una rama en serie con dos capacitores, C1 = 5µF y C2 = 10µF, y otra rama en paralelo con un capacitor, C3 = 20µF.
- Calcula la capacitancia equivalente de la rama en serie:
1/C_serie = 1/5µF + 1/10µF = 3/10µF
C_serie = 10µF/3 = 3.33µF
- Calcula la capacitancia equivalente del circuito completo:
C_total = C_serie + C3 = 3.33µF + 20µF = 23.33µF
- Ejemplo 2: Otro circuito mixto puede tener dos ramas en paralelo, cada una con dos capacitores en serie. La capacitancia equivalente de cada rama se calcula como en el ejemplo anterior. Luego, se suman las capacitancias equivalentes de las dos ramas para obtener la capacitancia equivalente total del circuito.
Ejercicios de Capacitores: Resolviendo Problemas
Ejercicios de Capacitores en Serie
- Ejercicio 1: Un circuito en serie contiene tres capacitores, C1 = 2µF, C2 = 4µF y C3 = 6µF. Calcula la capacitancia total del circuito.
- Ejercicio 2: Se aplica un voltaje de 12V a un circuito en serie con dos capacitores, C1 = 3µF y C2 = 6µF. Calcula la carga eléctrica en cada capacitor.
Ejercicios de Capacitores en Paralelo
- Ejercicio 1: Un circuito en paralelo contiene dos capacitores, C1 = 10µF y C2 = 20µF. Calcula la capacitancia total del circuito.
- Ejercicio 2: Se aplica un voltaje de 12V a un circuito en paralelo con dos capacitores, C1 = 3µF y C2 = 6µF. Calcula el voltaje en cada capacitor.
Ejercicios de Circuitos Mixtos
- Ejercicio 1: Un circuito mixto tiene dos ramas en paralelo. La primera rama contiene dos capacitores en serie, C1 = 5µF y C2 = 10µF. La segunda rama contiene un solo capacitor, C3 = 20µF. Calcula la capacitancia equivalente del circuito.
- Ejercicio 2: Se aplica un voltaje de 12V a un circuito mixto con dos ramas en serie. La primera rama contiene un capacitor, C1 = 5µF, y la segunda rama contiene dos capacitores en paralelo, C2 = 10µF y C3 = 20µF. Calcula la carga eléctrica en cada capacitor.
Aplicaciones de los Capacitores en Serie y Paralelo
Filtros de Frecuencia
Los capacitores pueden ser utilizados para construir filtros de frecuencia, que permiten el paso de ciertas frecuencias mientras bloquean otras. Por ejemplo, un filtro de paso bajo utiliza un capacitor en serie con una resistencia para permitir el paso de frecuencias bajas y bloquear las altas. Por otro lado, un filtro de paso alto utiliza un capacitor en paralelo con una resistencia para permitir el paso de frecuencias altas y bloquear las bajas.
Almacenamiento de Energía
Los capacitores pueden almacenar energía eléctrica, y su capacidad de almacenamiento depende de su capacitancia. Un capacitor en paralelo con una fuente de voltaje se carga hasta que alcanza el voltaje de la fuente. Esta energía almacenada se puede liberar posteriormente al circuito cuando la fuente se desconecta. En este caso, el capacitor actuará como una fuente de energía temporal.
Circuitos de Sincronización
Los capacitores se utilizan en circuitos de sincronización para controlar el tiempo de respuesta de un circuito. Por ejemplo, un circuito RC utiliza un capacitor y una resistencia para crear un retraso de tiempo. La duración del retraso depende de la resistencia y la capacitancia. Esta aplicación es crucial en la creación de temporizadores, osciladores y otros sistemas que requieren un control preciso del tiempo.
Los capacitores en serie y en paralelo son herramientas esenciales para el diseño y análisis de circuitos electrónicos. Dominar la teoría y las fórmulas para calcular la capacitancia equivalente de un circuito es fundamental para comprender el comportamiento de los circuitos y para realizar cálculos precisos.
Video sobre Capacitores en Serie y Paralelo: Formulas y Ejercicios Resueltos
Preguntas Frecuentes
¿Cómo se calcula la capacitancia total de un circuito de capacitores en paralelo?
La capacitancia total de un circuito de capacitores en paralelo se calcula sumando las capacitancias de cada capacitor individual. Esto significa que la capacitancia total es siempre mayor que la capacitancia del capacitor más grande del circuito. La fórmula es sencilla: C = C1 + C2 + C3 + … , donde C es la capacitancia total y C1, C2, C3, etc. son las capacitancias de cada capacitor individual.
¿Por qué la capacitancia total de un circuito en serie es menor que la capacitancia del capacitor más pequeño?
La capacitancia total de un circuito en serie es menor que la capacitancia del capacitor más pequeño debido a que los capacitores se oponen a la carga total. La fórmula 1/C = 1/C1 + 1/C2 + 1/C3 + … muestra cómo la capacitancia total disminuye a medida que se añaden más capacitores en serie. La carga eléctrica debe pasar a través de cada capacitor en serie para llegar al siguiente, lo que reduce la capacidad total del circuito de almacenar carga.
¿Cómo se calculan los circuitos mixtos de capacitores?
Para calcular la capacitancia equivalente de un circuito mixto de capacitores, primero debes identificar las ramas en serie y en paralelo. Luego, debes aplicar las fórmulas de capacitancia total para circuitos en serie y en paralelo de forma secuencial. Primero se calculan las capacitancias equivalentes de las ramas en serie, luego las de las ramas en paralelo, y así sucesivamente, hasta obtener la capacitancia equivalente total del circuito.
¿Qué son los filtros de frecuencia y cómo funcionan los capacitores en ellos?
Los filtros de frecuencia son circuitos que permiten el paso de ciertas frecuencias mientras bloquean otras. Los capacitores juegan un papel fundamental en los filtros de frecuencia, ya que su capacidad de bloquear o pasar las señales depende de la frecuencia. Por ejemplo, un capacitor en serie con una resistencia forma un filtro de paso bajo, mientras que un capacitor en paralelo con una resistencia forma un filtro de paso alto.
¿Dónde más se utilizan los capacitores en serie y en paralelo, además de los filtros de frecuencia?
Los capacitores en serie y en paralelo tienen muchas otras aplicaciones, como el almacenamiento de energía, los circuitos de sincronización, los circuitos de desacoplamiento y los circuitos de temporización. En los circuitos de almacenamiento de energía, un capacitor en paralelo con una fuente de voltaje se carga hasta que alcanza el voltaje de la fuente, y luego libera la energía almacenada cuando la fuente se desconecta. En los circuitos de sincronización, los capacitores se utilizan para controlar el tiempo de respuesta de un circuito, como en los circuitos RC, donde la duración del retraso depende de la resistencia y la capacitancia.
Concluyendo
Este viaje a través de los capacitores en serie y paralelo nos ha llevado a desentrañar las fórmulas que rigen su comportamiento, así como a poner en práctica nuestros conocimientos con ejemplos y ejercicios. Hemos visto cómo la unión de estos componentes puede generar efectos distintos, siendo la suma de sus capacitancias un valor que decrece en serie y aumenta en paralelo. De esta manera, la capacidad de almacenamiento de energía se ve modificada, abriendo un abanico de posibilidades para el diseño de filtros, sistemas de sincronización y circuitos que requieren un control preciso del tiempo. Al igual que los ríos que se dividen en canales, la corriente fluye a través de cada capacitor en serie, pero su «fuerza» se ve disminuida. En paralelo, sin embargo, la corriente se multiplica, dando como resultado un aumento de la capacidad total. En definitiva, la comprensión de estos conceptos nos acerca al fascinante mundo de la electrónica, donde cada elemento, como las piezas de un rompecabezas, juega un papel crucial en la creación de sistemas complejos y funcionales.
Compartelo
¡Descubre cómo funcionan los capacitores en serie y en paralelo! Este artículo te explica con detalle las fórmulas, las relaciones entre la corriente, la carga y la capacitancia total, y te ayudará a comprender cómo se comportan en un circuito. No te quedes con la duda, ¡dale un vistazo!
Lee También
Inductores en Serie y Paralelo: Guía Completa de Conexiones y Aplicaciones¡Comparte este conocimiento con tus amigos y colegas que también trabajan con circuitos!
capacitores #electronica #circuitos #fisica #ingenieria #aprendizaje #conocimiento
