Circuitos RLC en Paralelo: Análisis en Corriente Alterna y Mixtos

Adéntrate en el fascinante mundo de los circuitos RLC en paralelo, donde resistencias, inductancias y capacitancias se entrelazan en un baile eléctrico. En este análisis, exploraremos el comportamiento de estos circuitos bajo corriente alterna y también en escenarios mixtos, revelando las complejidades y las aplicaciones prácticas que los caracterizan.

Lectura Rápida

1. En un circuito RLC paralelo, la corriente total se divide en las ramas de la resistencia, la bobina y el capacitor.
2. La impedancia del circuito paralelo se calcula como la inversa de la suma de las admitancias de cada componente.
3. La resonancia ocurre cuando la impedancia es mínima y la corriente total es máxima.
4. La frecuencia de resonancia se determina por la inductancia y la capacitancia del circuito.
5. El ángulo de fase del circuito determina si la corriente lidera o se retrasa respecto a la tensión.
6. En circuitos RLC mixtos, se combinan componentes en serie y paralelo, lo que aumenta la complejidad del análisis.
7. Las aplicaciones de circuitos RLC paralelo incluyen filtros de frecuencia, osciladores y sistemas de comunicación.

Análisis de Circuitos RLC en Paralelo

Conceptos Básicos de Circuitos en Paralelo

Un circuito en paralelo es un circuito eléctrico donde dos o más componentes están conectados entre dos puntos comunes, de modo que la corriente tiene múltiples caminos para fluir. Cada componente en paralelo tiene la misma tensión aplicada, pero la corriente se divide entre cada rama del circuito.

En un circuito RLC en paralelo, la tensión aplicada es la misma en la resistencia (R), la bobina (L) y el condensador (C). La corriente total es la suma vectorial de las corrientes que fluyen a través de cada componente, considerando las diferencias de fase entre ellas.

Ley de Kirchhoff en Circuitos Paralelos

La ley de Kirchhoff de las corrientes, también conocida como la ley de nodos, establece que la suma algebraica de las corrientes que entran y salen de un nodo es igual a cero. En un circuito en paralelo, esto significa que la corriente total que entra en el circuito es igual a la suma de las corrientes que salen de cada rama del circuito.

Impedancia y Admitancia en Circuitos RLC Paralelo

Impedancia en Circuitos RLC en Paralelo

La impedancia (Z) es la resistencia al flujo de corriente en un circuito de corriente alterna (CA). En un circuito RLC en paralelo, la impedancia total es la inversa de la suma de las admitancias de cada componente.

La impedancia total del circuito se puede calcular mediante la siguiente fórmula:


Z = 1 / √(1/R² + (1/Xc - 1/Xl)²)


donde:

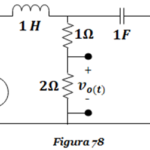Circuitos de Corriente Alterna: Guía Completa de R, L, C, RL, RC y RLC

• R es la resistencia
• Xc es la reactancia capacitiva
• Xl es la reactancia inductiva

Admitancia en Circuitos RLC en Paralelo

La admitancia (Y) es la inversa de la impedancia, y representa la facilidad con la que la corriente fluye a través de un circuito. En un circuito RLC en paralelo, la admitancia total es la suma de las admitancias de cada componente.

La admitancia total del circuito se puede calcular mediante la siguiente fórmula:


Y = 1/Z = √(1/R² + (1/Xc - 1/Xl)²)


Análisis de Circuitos RL, RC y RLC en Paralelo

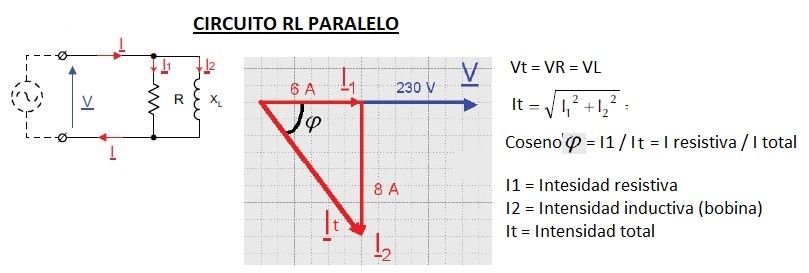
Circuito RL en Paralelo

Un circuito RL en paralelo consta de una resistencia (R) y una bobina (L) conectadas en paralelo. La impedancia del circuito RL en paralelo se calcula considerando la reactancia inductiva (Xl) de la bobina:


Z = 1 / √(1/R² + (1/Xl)²)


La corriente en la resistencia (Ir) es igual a la tensión aplicada (V) dividida por la resistencia (R). La corriente en la bobina (Il) es igual a la tensión aplicada (V) dividida por la reactancia inductiva (Xl). La corriente total (I) es la suma vectorial de las corrientes en la resistencia y la bobina.

Circuito RC en Paralelo

Un circuito RC en paralelo consta de una resistencia (R) y un condensador (C) conectados en paralelo. La impedancia del circuito RC en paralelo se calcula considerando la reactancia capacitiva (Xc) del condensador:

Contadores: Funcionamiento, Esquemas y Aplicaciones en Circuitos Eléctricos


Z = 1 / √(1/R² + (1/Xc)²)


La corriente en la resistencia (Ir) es igual a la tensión aplicada (V) dividida por la resistencia (R). La corriente en el condensador (Ic) es igual a la tensión aplicada (V) dividida por la reactancia capacitiva (Xc). La corriente total (I) es la suma vectorial de las corrientes en la resistencia y el condensador.

Circuito RLC en Paralelo

Un circuito RLC en paralelo consta de una resistencia (R), una bobina (L) y un condensador (C) conectados en paralelo. La impedancia del circuito RLC en paralelo se calcula considerando las reactancias inductiva (Xl) y capacitiva (Xc):


Z = 1 / √(1/R² + (1/Xc - 1/Xl)²)


La corriente en la resistencia (Ir) es igual a la tensión aplicada (V) dividida por la resistencia (R). La corriente en la bobina (Il) es igual a la tensión aplicada (V) dividida por la reactancia inductiva (Xl). La corriente en el condensador (Ic) es igual a la tensión aplicada (V) dividida por la reactancia capacitiva (Xc). La corriente total (I) es la suma vectorial de las corrientes en la resistencia, la bobina y el condensador.

Resonancia en Circuitos RLC en Paralelo

Frecuencia de Resonancia

La frecuencia de resonancia (fr) es la frecuencia a la que la impedancia del circuito RLC en paralelo es mínima y la corriente total es máxima. En esta frecuencia, la reactancia inductiva (Xl) es igual a la reactancia capacitiva (Xc):


fr = 1 / (2π√(LC))


donde:

Cortocircuito Eléctrico: Causas, Riesgos y Soluciones

• L es la inductancia de la bobina
• C es la capacitancia del condensador

Factores de Calidad (Q) y Ancho de Banda

El factor de calidad (Q) es una medida de la selectividad de un circuito RLC en paralelo. Cuanto mayor es el factor Q, más estrecha es la banda de frecuencias a la que el circuito responde. El factor Q se calcula como la relación entre la reactancia inductiva (Xl) o capacitiva (Xc) y la resistencia (R) a la frecuencia de resonancia:


Q = Xl/R = Xc/R


El ancho de banda (BW) es el rango de frecuencias alrededor de la frecuencia de resonancia en el que la corriente total es al menos la mitad de su valor máximo. El ancho de banda se calcula como la frecuencia de resonancia (fr) dividida por el factor de calidad (Q):


BW = fr/Q


Aplicaciones de Circuitos RLC en Paralelo

Filtros de Frecuencia

Los circuitos RLC en paralelo se utilizan como filtros de frecuencia. Un filtro pasa-bajas permite el paso de las frecuencias bajas y atenúa las frecuencias altas. Un filtro pasa-altas permite el paso de las frecuencias altas y atenúa las frecuencias bajas. Un filtro pasa-banda permite el paso de un rango específico de frecuencias y atenúa las frecuencias fuera de ese rango.

Circuitos de Sintonización

Los circuitos RLC en paralelo se utilizan en circuitos de sintonización, como en los receptores de radio. Al variar la capacitancia del condensador o la inductancia de la bobina, se puede ajustar la frecuencia de resonancia del circuito para seleccionar una frecuencia específica de una señal de radio.

Diagrama de Circuito Mixto: Guía Completa y Ejemplos

Circuitos de Acoplamiento

Los circuitos RLC en paralelo se utilizan en circuitos de acoplamiento, como en las antenas de radio. Un circuito de acoplamiento permite transferir energía de un circuito a otro.

Ejemplos Prácticos de Circuitos RLC en Paralelo

Ejemplo 1: Filtro Pasa-Bajas

Un filtro pasa-bajas simple se puede construir utilizando un circuito RLC en paralelo. En este circuito, la resistencia (R) se conecta en paralelo con la bobina (L) y el condensador (C). La frecuencia de corte del filtro pasa-bajas se determina por la inductancia (L) y la capacitancia (C) del circuito. Las frecuencias más bajas que la frecuencia de corte pasan a través del filtro, mientras que las frecuencias más altas son atenuadas.

Ejemplo 2: Circuito de Sintonización de Radio

Un circuito de sintonización de radio se puede construir utilizando un circuito RLC en paralelo. En este circuito, la bobina (L) y el condensador (C) están conectados en paralelo. La frecuencia de resonancia del circuito se ajusta variando la capacitancia del condensador. Cuando la frecuencia de la señal de radio coincide con la frecuencia de resonancia del circuito, la corriente en el circuito es máxima, y la señal se amplifica.

Ejemplo 3: Circuito de Acoplamiento de Antena

Un circuito de acoplamiento de antena se puede construir utilizando un circuito RLC en paralelo. En este circuito, la bobina (L) y el condensador (C) están conectados en paralelo. La frecuencia de resonancia del circuito se ajusta para que coincida con la frecuencia de la señal de radio que se va a transmitir o recibir. La bobina y el condensador actúan como un circuito resonante que transfiere energía de la antena al receptor o del receptor a la antena.

Análisis de Circuitos Mixtos RLC en Paralelo

Circuitos RLC en Paralelo con Resistencias en Serie

Un circuito RLC en paralelo con resistencias en serie se compone de una o más resistencias conectadas en serie con una rama del circuito paralelo, con la bobina (L) y el condensador (C) en la otra rama. La resistencia total en serie se calcula sumando las resistencias individuales. La impedancia total del circuito se calcula teniendo en cuenta la resistencia total en serie y la admitancia del circuito paralelo.

Circuito en Serie vs Paralelo: Cuadro Comparativo Completo

Circuitos RLC en Paralelo con Bobinas en Serie

Un circuito RLC en paralelo con bobinas en serie se compone de una o más bobinas conectadas en serie con una rama del circuito paralelo, con la resistencia (R) y el condensador (C) en la otra rama. La inductancia total en serie se calcula sumando las inductancias individuales. La impedancia total del circuito se calcula teniendo en cuenta la inductancia total en serie y la admitancia del circuito paralelo.

Circuitos RLC en Paralelo con Condensadores en Serie

Un circuito RLC en paralelo con condensadores en serie se compone de uno o más condensadores conectados en serie con una rama del circuito paralelo, con la resistencia (R) y la bobina (L) en la otra rama. La capacitancia total en serie se calcula mediante la siguiente fórmula:


1/Ctotal = 1/C1 + 1/C2 + ... + 1/Cn


La impedancia total del circuito se calcula teniendo en cuenta la capacitancia total en serie y la admitancia del circuito paralelo.

Herramientas para el Análisis de Circuitos RLC en Paralelo

Simulaciones por Computadora

Las simulaciones por computadora, como SPICE y Multisim, son herramientas potentes para el análisis de circuitos RLC en paralelo. Estas herramientas permiten al usuario crear modelos del circuito, establecer parámetros y simular el comportamiento del circuito en diferentes condiciones.

Análisis Matemático

El análisis matemático también se puede utilizar para analizar circuitos RLC en paralelo. Esto implica el uso de ecuaciones matemáticas para describir el comportamiento del circuito y resolver para las variables de interés.

Pruebas Experimentales

Las pruebas experimentales son una forma práctica de analizar circuitos RLC en paralelo. Esto implica la construcción de un prototipo del circuito y la medición de sus características usando instrumentos de medición.

Para profundizar en el análisis y diseño de circuitos RLC en paralelo, es recomendable consultar recursos especializados como el sitio web de Electronics Tutorials.

Video sobre Circuitos RLC en Paralelo: Análisis en Corriente Alterna y Mixtos

Preguntas Frecuentes

¿Cómo se calcula la corriente total en un circuito RLC en paralelo?

La corriente total en un circuito RLC en paralelo es la suma vectorial de las corrientes que fluyen a través de cada componente. Es decir, la corriente total no solo se calcula sumando las magnitudes de las corrientes individuales, sino que también se deben considerar las diferencias de fase entre ellas. Esto se debe a que la corriente en la bobina (L) y el condensador (C) no están en fase con la tensión aplicada, mientras que la corriente en la resistencia (R) sí lo está. Para realizar el cálculo, se pueden utilizar diagramas fasoriales o ecuaciones matemáticas que tengan en cuenta las fases de cada corriente.

¿Qué ocurre en un circuito RLC en paralelo cuando la frecuencia de la tensión aplicada coincide con la frecuencia de resonancia del circuito?

En esta situación, la impedancia del circuito alcanza su valor mínimo, lo que significa que la resistencia al flujo de corriente es mínima. Como consecuencia, la corriente total en el circuito alcanza su valor máximo. Este fenómeno se conoce como resonancia, y es una característica importante de los circuitos RLC en paralelo. En la frecuencia de resonancia, la reactancia inductiva (Xl) es igual a la reactancia capacitiva (Xc), lo que hace que la corriente en la bobina y el condensador se cancelen mutuamente, dejando solo la corriente en la resistencia.

¿Cómo influye el factor de calidad (Q) en el comportamiento de un circuito RLC en paralelo?

El factor de calidad (Q) es una medida de la selectividad del circuito. Un circuito con un factor Q alto es más selectivo, es decir, responde con mayor intensidad a una banda de frecuencias estrecha alrededor de la frecuencia de resonancia. Esto significa que el circuito "filtra" las señales que están fuera de esa banda de frecuencias. Por otro lado, un circuito con un factor Q bajo es menos selectivo, respondiendo con mayor intensidad a un rango más amplio de frecuencias. Un factor Q alto es deseable en aplicaciones como los receptores de radio, donde se quiere seleccionar una frecuencia específica de una señal de radio.

¿Qué es la admitancia en un circuito RLC en paralelo y cómo se relaciona con la impedancia?

La admitancia (Y) es la inversa de la impedancia (Z) y representa la facilidad con la que la corriente fluye a través de un circuito. En un circuito RLC en paralelo, la admitancia total es la suma de las admitancias de cada componente. Cuanto mayor es la admitancia, menor es la impedancia, lo que significa que la corriente fluye con mayor facilidad a través del circuito. La relación entre la admitancia y la impedancia es fundamental para el análisis de los circuitos RLC en paralelo, ya que permite calcular la corriente total en el circuito a partir de la impedancia o viceversa.

¿Cuáles son algunas de las aplicaciones más comunes de los circuitos RLC en paralelo?

Los circuitos RLC en paralelo tienen una amplia variedad de aplicaciones en electrónica, incluyendo:

• Filtros de frecuencia: se utilizan para permitir el paso de un rango específico de frecuencias y atenuar las frecuencias fuera de ese rango.
• Circuitos de sintonización: se utilizan en receptores de radio para seleccionar una frecuencia específica de una señal de radio.
• Circuitos de acoplamiento: se utilizan para transferir energía de un circuito a otro, como en las antenas de radio.
• Otros: también se utilizan en aplicaciones como el control de motores, la generación de señales y la detección de frecuencia.

Concluyendo

El análisis de circuitos RLC en paralelo revela un mundo fascinante donde la corriente se divide entre ramas, la impedancia se define por la admitancia, y la resonancia marca el punto de mayor corriente. Desde filtros de frecuencia hasta circuitos de sintonización y acoplamiento, estos circuitos son esenciales en la electrónica moderna. Su estudio, aunque complejo, nos permite comprender y controlar el flujo de energía, abriendo un camino hacia la innovación tecnológica.

Compartelo

¡Descubre los secretos de los Circuitos RLC en Paralelo! Este artículo te guiará a través de la complejidad de la corriente alterna y los circuitos mixtos, desentrañando las relaciones entre resistencias, bobinas y condensadores. ¡Aprende cómo calcular intensidades, tensiones y comprender la importancia de la admitancia e impedancia!

No te quedes con la duda, ¡Comparte este conocimiento con tus amigos y colegas! Juntos, podremos construir un mundo más brillante con la electricidad.

#CircuitosRLC #CorrienteAlterna #Electrotecnia #Ingeniería #Ciencia