Ejercicios Resueltos de Corriente Alterna: Circuitos RLC en Serie y Paralelo

El mundo de la electricidad se torna fascinante al explorar el comportamiento de la corriente alterna, especialmente en circuitos RLC. Descubrir la sinergia entre resistencias, inductancias y capacitancias en estas configuraciones series y paralelas, nos introduce en un universo de fenómenos electromagnéticos que regulan nuestro entorno.
Adentrarse en la resolución de ejercicios de corriente alterna es la mejor forma de comprender y dominar estas dinámicas, abriendo las puertas a un entendimiento profundo del funcionamiento de dispositivos electrónicos que utilizamos a diario.

Resumen Clave

• El artículo explora los circuitos RLC en serie y paralelo, fundamentales en la comprensión de la corriente alterna.
• Se presentan ejercicios resueltos que ilustran el cálculo de la impedancia, la corriente y la potencia en circuitos RLC.
• Se aborda el concepto de resonancia en circuitos RLC, donde la impedancia es mínima y la corriente máxima.
• Se muestra cómo la reactancia capacitiva y la reactancia inductiva influyen en la impedancia total del circuito.
• Se explica el uso de diagramas fasoriales para representar las relaciones de fase entre la corriente y la tensión.
• Se proporcionan ejemplos prácticos de aplicaciones de circuitos RLC, como filtros de frecuencia.

Circuitos RL: Análisis en Corriente Alterna

Impedancia de un circuito RL

Imagina un circuito que contiene una resistencia (R) y una bobina (L) conectadas en serie. En corriente alterna, la bobina presenta una oposición al flujo de corriente llamada reactancia inductiva (XL), que depende de la frecuencia (f) y la inductancia (L):

XL = 2πfL

La impedancia total (Z) del circuito RL es la combinación vectorial de la resistencia y la reactancia inductiva. Puedes calcularla utilizando el teorema de Pitágoras:

Z = √(R² + XL²)

La impedancia del circuito RL no solo afecta la magnitud de la corriente, sino también su fase. La corriente en un circuito RL se retrasa con respecto a la tensión debido a la presencia de la bobina.

Cálculo de la Corriente y la Potencia

Para calcular la corriente (I) en un circuito RL, puedes utilizar la ley de Ohm:

I = V/Z

Donde V es la tensión aplicada al circuito.

La potencia (P) disipada en un circuito RL es la potencia real que se disipa en la resistencia:

Lee TambiénElectric Box 2: Resuelve Circuitos y Desafía Tu Lógica

P = I²R

La potencia reactiva (Q) almacenada en la bobina se calcula como:

Q = I²XL

La potencia aparente (S) es la combinación vectorial de la potencia real y la potencia reactiva:

S = √(P² + Q²)

Ejemplos de ejercicios corriente alterna RL

Ejercicio 1: Un circuito RL tiene una resistencia de 100 Ω y una bobina de 0.1 H. Si se aplica una tensión de 120 V a 60 Hz, calcula la impedancia, la corriente y la potencia del circuito.

Solución:

1. Calcula la reactancia inductiva:

   XL = 2πfL = 2π(60 Hz)(0.1 H) = 37.7 Ω

2. Calcula la impedancia:

   Z = √(R² + XL²) = √(100² + 37.7²) = 106.1 Ω

3. Calcula la corriente:

   I = V/Z = 120 V / 106.1 Ω = 1.13 A

4. Calcula la potencia real:

   P = I²R = (1.13 A)²(100 Ω) = 128 W

5. Calcula la potencia reactiva:

   Q = I²XL = (1.13 A)²(37.7 Ω) = 48.1 VAR

6. Calcula la potencia aparente:

   S = √(P² + Q²) = √(128² + 48.1²) = 137 VA

Ejercicio 2: Un circuito RL tiene una impedancia de 50 Ω y una corriente de 2 A. Si la frecuencia de la fuente de tensión es de 50 Hz, calcula la inductancia de la bobina.

Lee También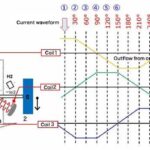Guía Completa de Motores Trifásicos: Funcionamiento, Conexión y Control

Solución:

1. Calcula la reactancia inductiva utilizando la relación entre la impedancia, la resistencia y la reactancia:

   XL = √(Z² – R²) = √(50² – 40²) = 30 Ω

2. Calcula la inductancia:

   L = XL / (2πf) = 30 Ω / (2π(50 Hz)) = 0.0955 H

Ejercicio 3: Un circuito RL tiene una resistencia de 20 Ω y una bobina de 0.05 H. Si se aplica una tensión de 100 V a 50 Hz, calcula la fase del ángulo de corriente con respecto a la tensión.

Solución:

1. Calcula la reactancia inductiva:

   XL = 2πfL = 2π(50 Hz)(0.05 H) = 15.7 Ω

2. Calcula el ángulo de fase:

   Φ = arctan(XL/R) = arctan(15.7 Ω / 20 Ω) = 38.2°

El ángulo de fase de 38.2° indica que la corriente se retrasa con respecto a la tensión en ese ángulo.

Circuitos RC: Análisis en Corriente Alterna

Impedancia de un circuito RC

Un circuito RC en corriente alterna consiste en una resistencia (R) y un condensador (C) conectados en serie. El condensador presenta una oposición al flujo de corriente llamada reactancia capacitiva (XC), que es inversamente proporcional a la frecuencia (f) y la capacitancia (C):

XC = 1 / (2πfC)

La impedancia total (Z) del circuito RC se calcula utilizando el teorema de Pitágoras:

Z = √(R² + XC²)

La impedancia del circuito RC afecta la magnitud y la fase de la corriente. La corriente en un circuito RC se adelanta con respecto a la tensión debido a la presencia del condensador.

Fase de la Corriente y la Tensión

En un circuito RC, la corriente se adelanta a la tensión en un ángulo de fase (Φ) que se calcula como:

Φ = arctan(-XC/R)

El signo negativo indica que la corriente se adelanta a la tensión.

Ejemplos de ejercicios corriente alterna RC

Ejercicio 1: Un circuito RC tiene una resistencia de 50 Ω y un condensador de 10 µF. Si se aplica una tensión de 120 V a 60 Hz, calcula la impedancia, la corriente y la fase del circuito.

Solución:

1. Calcula la reactancia capacitiva:

   XC = 1 / (2πfC) = 1 / (2π(60 Hz)(10 µF)) = 265.3 Ω

2. Calcula la impedancia:

   Z = √(R² + XC²) = √(50² + 265.3²) = 270.2 Ω

3. Calcula la corriente:

   I = V/Z = 120 V / 270.2 Ω = 0.44 A

4. Calcula la fase del circuito:

   Φ = arctan(-XC/R) = arctan(-265.3 Ω / 50 Ω) = -79.4°

La fase de -79.4° indica que la corriente se adelanta a la tensión en 79.4°.

Ejercicio 2: Un circuito RC tiene una impedancia de 100 Ω y una corriente de 0.5 A. Si la capacitancia del condensador es de 20 µF, calcula la frecuencia de la fuente de tensión.

Solución:

1. Calcula la reactancia capacitiva utilizando la relación entre la impedancia, la resistencia y la reactancia:

   XC = √(Z² – R²) = √(100² – 80²) = 60 Ω

2. Calcula la frecuencia:

   f = 1 / (2πCXC) = 1 / (2π(20 µF)(60 Ω)) = 132.6 Hz

Ejercicio 3: Un circuito RC tiene una resistencia de 30 Ω y un condensador de 5 µF. Si la tensión aplicada es de 100 V y la corriente es de 1 A, calcula la frecuencia de la fuente de tensión.

Solución:

1. Calcula la impedancia:

   Z = V/I = 100 V / 1 A = 100 Ω

2. Calcula la reactancia capacitiva utilizando la relación entre la impedancia, la resistencia y la reactancia:

   XC = √(Z² – R²) = √(100² – 30²) = 95.4 Ω

3. Calcula la frecuencia:

   f = 1 / (2πCXC) = 1 / (2π(5 µF)(95.4 Ω)) = 334.5 Hz

Circuitos RLC en Serie: Análisis en Corriente Alterna

Impedancia Total del Circuito

En un circuito RLC en serie, la resistencia (R), la bobina (L) y el condensador (C) se encuentran conectados en serie. La impedancia total (Z) del circuito es la combinación vectorial de la resistencia, la reactancia inductiva (XL) y la reactancia capacitiva (XC):

Z = √(R² + (XL – XC)²)

La impedancia del circuito RLC en serie afecta la magnitud y la fase de la corriente. La corriente en un circuito RLC en serie puede adelantarse o retrasarse con respecto a la tensión, dependiendo de la relación entre la reactancia inductiva y la reactancia capacitiva.

Resonancia en Circuitos RLC en Serie

La resonancia en un circuito RLC en serie ocurre cuando la reactancia inductiva (XL) es igual a la reactancia capacitiva (XC). En este punto, la impedancia del circuito es mínima y la corriente alcanza su máximo valor. La frecuencia de resonancia (fr) se calcula como:

fr = 1 / (2π√(LC))

En la resonancia, la corriente y la tensión están en fase, lo que significa que el ángulo de fase (Φ) es cero.

Cálculo de la Corriente y la Potencia

La corriente (I) en un circuito RLC en serie se calcula utilizando la ley de Ohm:

I = V/Z

La potencia real (P) disipada en el circuito RLC en serie es la potencia disipada en la resistencia:

P = I²R

La potencia reactiva (Q) almacenada en la bobina y el condensador se calcula como:

Q = I²(XL – XC)

La potencia aparente (S) es la combinación vectorial de la potencia real y la potencia reactiva:

S = √(P² + Q²)

Ejemplos de ejercicios corriente alterna RLC en serie

Ejercicio 1: Un circuito RLC en serie tiene una resistencia de 10 Ω, una bobina de 0.1 H y un condensador de 10 µF. Si se aplica una tensión de 120 V a 60 Hz, calcula la impedancia, la corriente, la potencia real y la potencia reactiva del circuito.

Solución:

1. Calcula la reactancia inductiva:

   XL = 2πfL = 2π(60 Hz)(0.1 H) = 37.7 Ω

2. Calcula la reactancia capacitiva:

   XC = 1 / (2πfC) = 1 / (2π(60 Hz)(10 µF)) = 265.3 Ω

3. Calcula la impedancia:

   Z = √(R² + (XL – XC)²) = √(10² + (37.7 – 265.3)²) = 227.6 Ω

4. Calcula la corriente:

   I = V/Z = 120 V / 227.6 Ω = 0.53 A

5. Calcula la potencia real:

   P = I²R = (0.53 A)²(10 Ω) = 2.81 W

6. Calcula la potencia reactiva:

   Q = I²(XL – XC) = (0.53 A)²(37.7 – 265.3) = -25.7 VAR

El signo negativo de la potencia reactiva indica que la potencia reactiva es capacitiva.

Ejercicio 2: Un circuito RLC en serie tiene una frecuencia de resonancia de 1000 Hz. Si la bobina tiene una inductancia de 0.1 H, calcula la capacitancia del condensador.

Solución:

1. Calcula la capacitancia utilizando la fórmula de la frecuencia de resonancia:

   C = 1 / (4π²f²L) = 1 / (4π²(1000 Hz)²(0.1 H)) = 2.53 µF

Ejercicio 3: Un circuito RLC en serie tiene una resistencia de 50 Ω, una bobina de 0.05 H y un condensador de 10 µF. Si se aplica una tensión de 100 V a 50 Hz, calcula la fase del ángulo de corriente con respecto a la tensión.

Solución:

1. Calcula la reactancia inductiva:

   XL = 2πfL = 2π(50 Hz)(0.05 H) = 15.7 Ω

2. Calcula la reactancia capacitiva:

   XC = 1 / (2πfC) = 1 / (2π(50 Hz)(10 µF)) = 318.3 Ω

3. Calcula el ángulo de fase:

   Φ = arctan((XL – XC)/R) = arctan((15.7 – 318.3) / 50) = -80.5°

El ángulo de fase de -80.5° indica que la corriente se adelanta a la tensión en 80.5°.

Circuitos RLC en Paralelo: Análisis en Corriente Alterna

Impedancia Total del Circuito

En un circuito RLC en paralelo, la resistencia (R), la bobina (L) y el condensador (C) están conectados en paralelo. La impedancia total (Z) del circuito se calcula utilizando la siguiente fórmula:

1/Z = √(1/R² + (1/XL – 1/XC)²)

La impedancia del circuito RLC en paralelo afecta la magnitud y la fase de la corriente. La corriente total en un circuito RLC en paralelo es la suma vectorial de las corrientes que fluyen a través de cada rama.

Resonancia en Circuitos RLC en Paralelo

La resonancia en un circuito RLC en paralelo ocurre cuando la reactancia inductiva (XL) es igual a la reactancia capacitiva (XC). En este punto, la impedancia del circuito es máxima y la corriente total es mínima. La frecuencia de resonancia (fr) se calcula como:

fr = 1 / (2π√(LC))

En la resonancia, la corriente total y la tensión están en fase, lo que significa que el ángulo de fase (Φ) es cero.

Cálculo de la Corriente y la Potencia

La corriente total (I) en un circuito RLC en paralelo se calcula utilizando la ley de Ohm:

I = V/Z

La corriente en cada rama se calcula utilizando la ley de Ohm para cada elemento:

IR = V/R

IL = V/XL

IC = V/XC

La potencia real (P) disipada en el circuito RLC en paralelo es la potencia disipada en la resistencia:

P = I²R

La potencia reactiva (Q) almacenada en la bobina y el condensador se calcula como:

Q = I²(XL – XC)

La potencia aparente (S) es la combinación vectorial de la potencia real y la potencia reactiva:

S = √(P² + Q²)

Ejemplos de ejercicios corriente alterna RLC en paralelo

Ejercicio 1: Un circuito RLC en paralelo tiene una resistencia de 100 Ω, una bobina de 0.1 H y un condensador de 10 µF. Si se aplica una tensión de 120 V a 60 Hz, calcula la impedancia, la corriente total, la corriente en cada rama, la potencia real y la potencia reactiva del circuito.

Solución:

1. Calcula la reactancia inductiva:

   XL = 2πfL = 2π(60 Hz)(0.1 H) = 37.7 Ω

2. Calcula la reactancia capacitiva:

   XC = 1 / (2πfC) = 1 / (2π(60 Hz)(10 µF)) = 265.3 Ω

3. Calcula la impedancia:

   1/Z = √(1/R² + (1/XL – 1/XC)²) = √(1/100² + (1/37.7 – 1/265.3)²)
   Z = 97.6 Ω

4. Calcula la corriente total:

   I = V/Z = 120 V / 97.6 Ω = 1.23 A

5. Calcula la corriente en cada rama:

   IR = V/R = 120 V / 100 Ω = 1.2 A
   IL = V/XL = 120 V / 37.7 Ω = 3.19 A
   IC = V/XC = 120 V / 265.3 Ω = 0.45 A

6. Calcula la potencia real:

   P = I²R = (1.23 A)²(100 Ω) = 151.3 W

7. Calcula la potencia reactiva:

   Q = I²(XL – XC) = (1.23 A)²(37.7 – 265.3) = -304.6 VAR

El signo negativo de la potencia reactiva indica que la potencia reactiva es capacitiva.

Ejercicio 2: Un circuito RLC en paralelo tiene una frecuencia de resonancia de 500 Hz. Si la capacitancia del condensador es de 20 µF, calcula la inductancia de la bobina.

Solución:

1. Calcula la inductancia utilizando la fórmula de la frecuencia de resonancia:

   L = 1 / (4π²f²C) = 1 / (4π²(500 Hz)²(20 µF)) = 0.0318 H

Ejercicio 3: Un circuito RLC en paralelo tiene una resistencia de 50 Ω, una bobina de 0.05 H y un condensador de 10 µF. Si se aplica una tensión de 100 V a 50 Hz, calcula la fase del ángulo de corriente con respecto a la tensión.

Solución:

1. Calcula la reactancia inductiva:

   XL = 2πfL = 2π(50 Hz)(0.05 H) = 15.7 Ω

2. Calcula la reactancia capacitiva:

   XC = 1 / (2πfC) = 1 / (2π(50 Hz)(10 µF)) = 318.3 Ω

3. Calcula el ángulo de fase:

   Φ = arctan((1/XL – 1/XC)/ (1/R)) = arctan((1/15.7 – 1/318.3) / (1/50)) = 71.6°

El ángulo de fase de 71.6° indica que la corriente se adelanta a la tensión en 71.6°.

Aplicaciones Prácticas de Circuitos RLC

Filtros de Frecuencia

Los circuitos RLC se utilizan ampliamente como filtros de frecuencia en electrónica. Un filtro de frecuencia permite el paso de ciertas frecuencias mientras bloquea otras. Los filtros RLC pueden ser de paso bajo, paso alto, paso banda o banda eliminada, dependiendo de la disposición de los componentes R, L y C.

• Filtro de paso bajo: Permite el paso de frecuencias bajas y bloquea las frecuencias altas.
• Filtro de paso alto: Permite el paso de frecuencias altas y bloquea las frecuencias bajas.
• Filtro de paso banda: Permite el paso de un rango específico de frecuencias y bloquea las frecuencias fuera de ese rango.
• Filtro de banda eliminada: Bloquea un rango específico de frecuencias y permite el paso de las frecuencias fuera de ese rango.

Circuitos de Acoplamiento

Los circuitos RLC también se utilizan para acoplar señales entre diferentes partes de un circuito o entre diferentes dispositivos. El acoplamiento se realiza mediante el uso de una bobina resonante, que selecciona la frecuencia de la señal que se va a acoplar.

Osciladores y Resonadores

Los circuitos RLC se pueden utilizar para crear osciladores y resonadores. Un oscilador produce una señal sinusoidal a una frecuencia específica. Un resonador amplifica una señal sinusoidal a una frecuencia específica.

Los osciladores y resonadores RLC se utilizan en una amplia variedad de aplicaciones, como radios, relojes, sensores y sistemas de control.

Ejemplos de Aplicaciones Prácticas

• Radio: Los circuitos RLC se utilizan en los receptores de radio para seleccionar la frecuencia de una estación de radio específica.
• Relojes: Los circuitos RLC se utilizan en los relojes de cuarzo para generar una señal de frecuencia precisa.
• Sensores: Los circuitos RLC se utilizan en los sensores para detectar cambios en la frecuencia de una señal, lo que permite medir parámetros como la temperatura, la presión y el flujo.
• Sistemas de control: Los circuitos RLC se utilizan en los sistemas de control para estabilizar el funcionamiento de los sistemas.

Recursos Adicionales para ejercicios corriente alterna

Para profundizar en el análisis de los circuitos RLC, te recomiendo consultar recursos como:

• Curso de Electricidad: https://www.coursera.org/specializations/electrical-engineering
• Libro de texto de circuitos eléctricos: «Análisis de Circuitos Eléctricos» por Nilsson y Riedel.

Recuerda que los circuitos RLC son componentes fundamentales de la electrónica moderna y la comprensión de su comportamiento te ayudará a diseñar y analizar una variedad de sistemas electrónicos.

Video sobre Ejercicios Resueltos de Corriente Alterna: Circuitos RLC en Serie y Paralelo

Preguntas Frecuentes

¿Qué es la impedancia en un circuito RL y cómo se relaciona con la resistencia y la reactancia inductiva?

La impedancia (Z) en un circuito RL es la oposición total al flujo de corriente alterna. Se compone de dos partes: la resistencia (R), que representa la oposición al flujo de corriente debido al material del conductor, y la reactancia inductiva (XL), que representa la oposición al flujo de corriente debido a la bobina. La impedancia se calcula como la raíz cuadrada de la suma de los cuadrados de la resistencia y la reactancia inductiva: Z = √(R² + XL²).

La impedancia no solo afecta la magnitud de la corriente, sino también su fase. Debido a la presencia de la bobina, la corriente en un circuito RL se retrasa con respecto a la tensión aplicada. La relación entre la impedancia, la resistencia y la reactancia inductiva es fundamental para comprender el comportamiento del circuito RL en corriente alterna.

¿Cómo se calcula la corriente en un circuito RL en corriente alterna?

La corriente en un circuito RL se calcula utilizando la ley de Ohm, pero con la impedancia (Z) en lugar de la resistencia: I = V/Z. La impedancia se calcula como se mencionó anteriormente, teniendo en cuenta la resistencia (R) y la reactancia inductiva (XL) del circuito.

Es importante recordar que la corriente en un circuito RL no es constante, sino que varía con el tiempo y se retrasa con respecto a la tensión aplicada. El ángulo de fase entre la corriente y la tensión depende de la relación entre la resistencia y la reactancia inductiva.

¿Qué tipos de problemas se pueden resolver utilizando los conocimientos de circuitos RL en corriente alterna?

Los conocimientos sobre circuitos RL en corriente alterna son esenciales para resolver una variedad de problemas prácticos en la ingeniería eléctrica y electrónica. Algunos ejemplos incluyen:

• Diseño de filtros de paso bajo: Los circuitos RL se utilizan para filtrar frecuencias bajas, permitiendo el paso de señales de baja frecuencia y bloqueando las de alta frecuencia.
• Análisis de sistemas de transmisión de energía: La inductancia de las líneas de transmisión de energía afecta el flujo de corriente y la eficiencia del sistema.
• Diseño de motores eléctricos: Los motores eléctricos utilizan bobinas para generar campos magnéticos que hacen girar el rotor. La inductancia de estas bobinas afecta el rendimiento del motor.
• Diseño de circuitos de conmutación: Los circuitos de conmutación utilizan bobinas para almacenar energía y controlar el flujo de corriente. La inductancia de estas bobinas afecta la velocidad de conmutación y la eficiencia del circuito.

¿Qué es la potencia reactiva en un circuito RL y cómo se relaciona con la potencia real y la potencia aparente?

La potencia reactiva (Q) en un circuito RL es la energía que se almacena y se libera periódicamente en el campo magnético de la bobina. Se mide en voltios-amperios reactivos (VAR). La potencia real (P) es la energía que se disipa en la resistencia del circuito y se mide en vatios (W). La potencia aparente (S) es la combinación vectorial de la potencia real y la potencia reactiva y se mide en voltios-amperios (VA).

La relación entre estas tres potencias se puede representar mediante un triángulo de potencia. La potencia real es el lado adyacente del triángulo, la potencia reactiva es el lado opuesto y la potencia aparente es la hipotenusa. La potencia aparente representa la potencia total que se suministra al circuito, mientras que la potencia real es la potencia útil que se disipa.

¿Cómo se puede calcular la frecuencia de resonancia en un circuito RLC en serie?

La frecuencia de resonancia (fr) en un circuito RLC en serie es la frecuencia a la que la reactancia inductiva (XL) es igual a la reactancia capacitiva (XC). En este punto, la impedancia del circuito es mínima y la corriente alcanza su máximo valor. La frecuencia de resonancia se calcula utilizando la siguiente fórmula:

fr = 1 / (2π√(LC))

donde L es la inductancia de la bobina y C es la capacitancia del condensador.

La frecuencia de resonancia es un parámetro importante para el diseño de circuitos RLC, ya que determina la frecuencia a la que el circuito tendrá su máxima respuesta. La resonancia se utiliza en una variedad de aplicaciones, como radios, filtros de frecuencia y circuitos de oscilación.

Para Concluir

En este recorrido por los circuitos RL, RC y RLC, hemos desentrañado las complejidades de la corriente alterna en cada configuración. Desde la impedancia que limita el flujo hasta la resonancia que amplifica la corriente, cada circuito ofrece un universo de posibilidades, como un lienzo en blanco para la innovación tecnológica. El dominio de estos conceptos abre las puertas a la comprensión de filtros de frecuencia, sistemas de acoplamiento y la construcción de osciladores, un testimonio de la versatilidad de la corriente alterna en el mundo de la electrónica.

Compartelo

¡Domina los circuitos de corriente alterna RLC con este invaluable recurso! ⚡ Aquí encontrarás una serie de ejercicios resueltos que te guiarán paso a paso por el análisis de circuitos RL, RC y RLC en serie y paralelo. ¡No pierdas la oportunidad de comprender a fondo el comportamiento de estos circuitos!

¿Quieres mejorar tus habilidades en electricidad? Comparte este contenido con tus compañeros de estudio o con cualquier persona que esté interesada en el fascinante mundo de la corriente alterna. ¡Ayúdanos a difundir este conocimiento!

¡Comparte el enlace con tus amigos y familiares en las redes sociales!

[Enlace al contenido]