Cálculo de Vigas Fácil: Sumatoria de Momentos y Diagramas de Esfuerzos

El cálculo de vigas puede ser un proceso complejo, pero con la ayuda de herramientas como la sumatoria de momentos, podemos simplificar el análisis y determinar con precisión los esfuerzos internos que actúan sobre la estructura. Entender cómo funciona la sumatoria de momentos nos abre las puertas a un mundo de posibilidades, permitiéndonos crear estructuras seguras y eficientes.

Lectura Rápida

1. El concepto de sumatoria de momentos es fundamental para el análisis de vigas en mecánica estructural, permitiendo determinar las fuerzas internas que actúan en la viga.
2. El método de sumatoria de momentos se basa en la aplicación de la segunda ley de Newton para cuerpos rígidos, utilizando la ecuación de equilibrio de momentos.
3. La sumatoria de momentos se utiliza para calcular las reacciones en los apoyos de la viga, que son las fuerzas que la viga ejerce sobre los apoyos.
4. Los diagramas de esfuerzos, como el diagrama de fuerzas cortantes y el diagrama de momentos flectores, se obtienen a partir de la sumatoria de momentos y proporcionan información sobre la distribución de las fuerzas internas.
5. Para realizar la sumatoria de momentos, se considera un punto de referencia arbitrario y se suman los momentos de todas las fuerzas que actúan sobre la viga respecto a ese punto.
6. La sumatoria de momentos debe ser igual a cero para que la viga se encuentre en equilibrio estático.
7. El método de sumatoria de momentos se aplica para determinar los esfuerzos en diferentes secciones de la viga, permitiendo analizar su comportamiento.
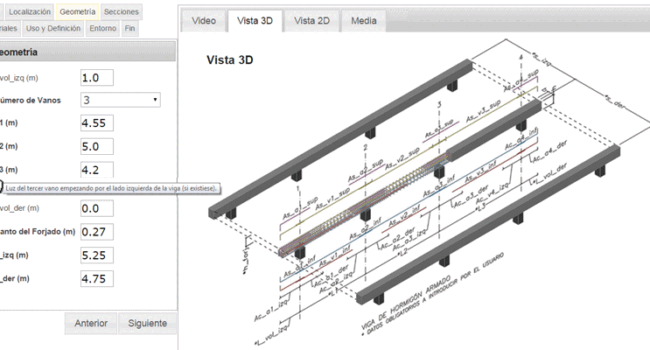
8. El cálculo de vigas se simplifica mediante el uso de software especializado que permite calcular la sumatoria de momentos y generar diagramas de esfuerzos.

Cálculo de Reacciones en Vigas

Ecuación de Equilibrio de Momentos

Para analizar el comportamiento de una viga, es fundamental comprender cómo se distribuyen las fuerzas y los momentos a lo largo de su estructura. En este contexto, la sumatoria de momentos juega un papel crucial.

La sumatoria de momentos, también conocida como sumatorio de momentos, es la suma algebraica de los momentos de todas las fuerzas que actúan sobre un cuerpo rígido. En términos simples, es la suma de las fuerzas multiplicadas por sus distancias al punto de referencia. Esta suma debe ser igual a cero para que el cuerpo esté en equilibrio estático.

En el caso de una viga, las reacciones en los apoyos son fuerzas que se generan para contrarrestar las cargas externas que actúan sobre la misma. Para determinar estas reacciones, se aplica la ecuación de equilibrio de momentos, que establece que la sumatoria de momentos alrededor de cualquier punto debe ser igual a cero.

La ecuación de equilibrio de momentos se expresa matemáticamente como:

∑M = 0

Donde:

• ∑M es la sumatoria de momentos
• M es el momento de cada fuerza

Para calcular el momento de una fuerza, se multiplica la magnitud de la fuerza por la distancia perpendicular al punto de referencia.

Recuerda que el signo del momento depende de la dirección del giro que produce la fuerza. Si el giro es en sentido contrario a las agujas del reloj, el momento es positivo. Si el giro es en sentido de las agujas del reloj, el momento es negativo.

Ejemplo Práctico de Reacciones en Vigas

Imagina una viga simplemente apoyada con una carga puntual en el centro. La viga tiene una longitud de L y la carga puntual es de P. Para calcular las reacciones en los apoyos, podemos utilizar la ecuación de equilibrio de momentos.

Cálculo de Vigas de Acero: Guía Completa y Paso a Paso

En este caso, tomaremos el punto de referencia en uno de los apoyos. La fuerza de reacción en el otro apoyo se considera desconocida.

Aplicaremos la ecuación de equilibrio de momentos:

∑M = 0

Entonces, la sumatoria de momentos en este caso sería:

• Momento de la carga puntual: P * (L/2) (negativo porque genera un giro en sentido de las agujas del reloj)
• Momento de la reacción en el otro apoyo: Ry * L (positivo porque genera un giro en sentido contrario a las agujas del reloj)

Combinando estos momentos, obtenemos la siguiente ecuación:

P * (L/2) - Ry * L = 0

Resolviendo para Ry, obtenemos:

Ry = P/2

De esta manera, hemos calculado la reacción en el apoyo opuesto a la carga puntual.

El cálculo de la reacción en el otro apoyo se puede realizar utilizando la ecuación de equilibrio de fuerzas verticales, que establece que la suma de todas las fuerzas verticales debe ser igual a cero.

Tipos de Puentes: Construcción y Características

Diagramas de Esfuerzos y Momentos

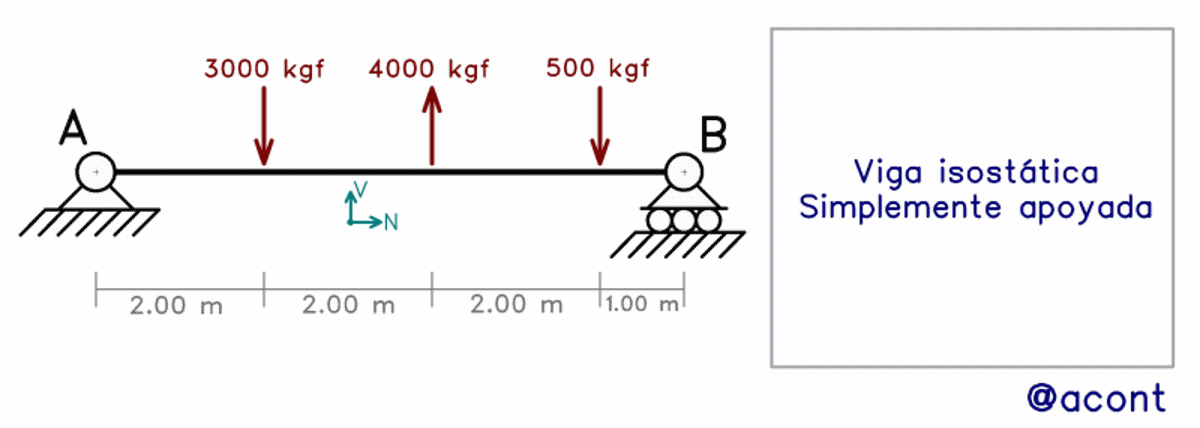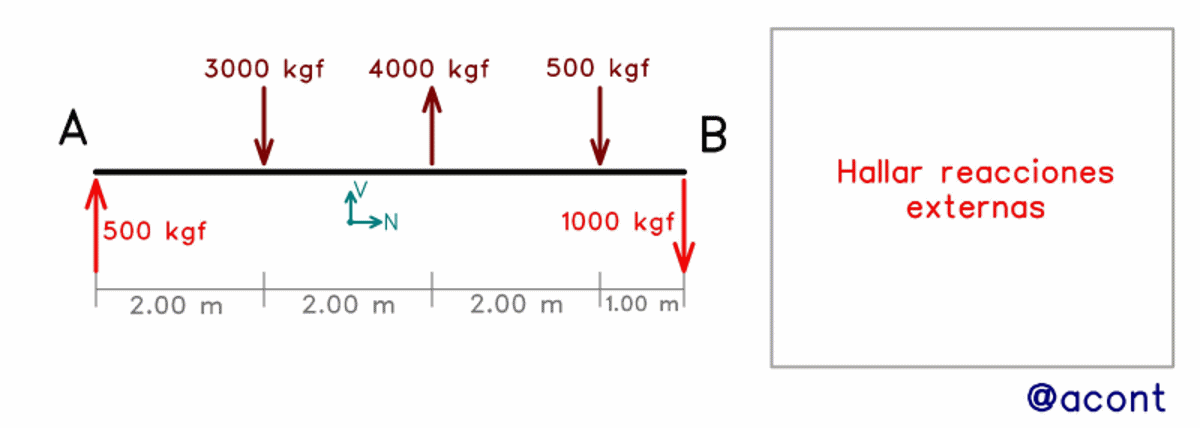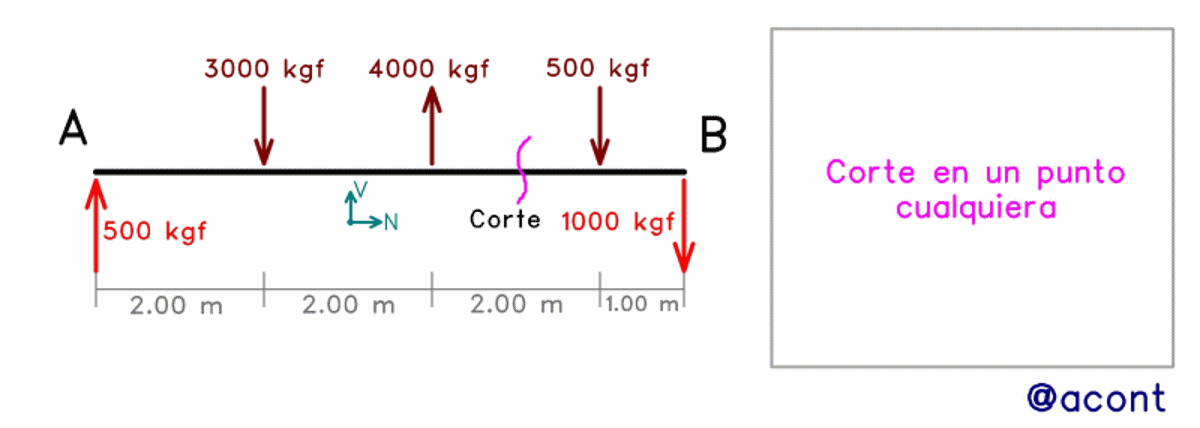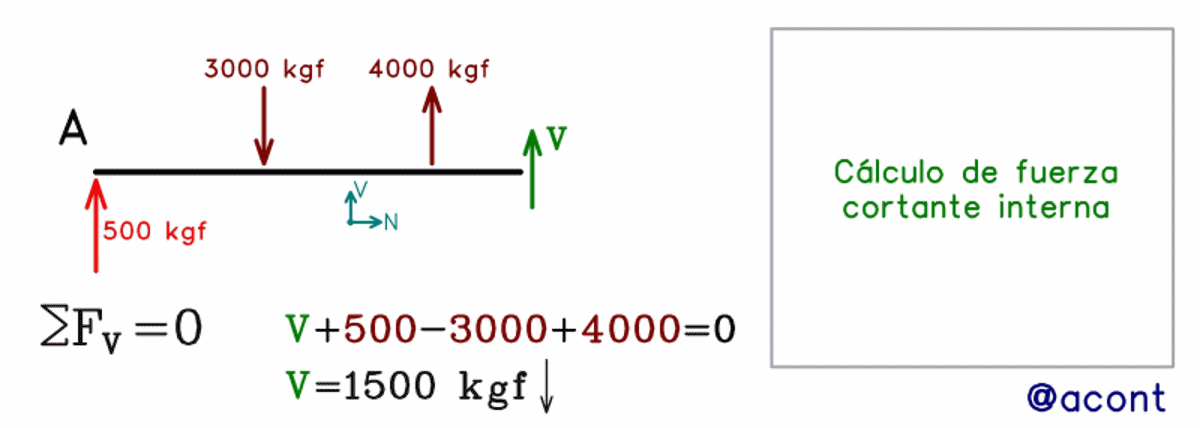
Diagrama de Esfuerzos Cortantes

El diagrama de esfuerzos cortantes representa la variación del esfuerzo cortante interno a lo largo de la viga. El esfuerzo cortante interno es la fuerza interna que actúa perpendicular a la sección transversal de la viga.

El diagrama de esfuerzos cortantes se construye graficando el esfuerzo cortante interno en función de la posición a lo largo de la viga. La forma del diagrama depende de las cargas que actúan sobre la viga y de la posición de los apoyos.

Diagrama de Momentos Flectores

El diagrama de momentos flectores representa la variación del momento flector interno a lo largo de la viga. El momento flector interno es el momento que actúa sobre una sección transversal de la viga, causado por las fuerzas externas.

El diagrama de momentos flectores se construye graficando el momento flector interno en función de la posición a lo largo de la viga. La forma del diagrama depende de las cargas que actúan sobre la viga y de la posición de los apoyos.

Carga Repartida Uniforme

Conversión a Fuerza Concentrada

En muchas ocasiones, la carga sobre una viga no se aplica en un punto específico, sino que se distribuye uniformemente a lo largo de un tramo de la viga. En este caso, hablamos de una carga repartida uniforme.

Para simplificar el cálculo de reacciones y diagramas de esfuerzos y momentos, es útil convertir la carga repartida uniforme en una fuerza concentrada equivalente.

La fuerza concentrada equivalente se obtiene multiplicando la carga repartida uniforme por la longitud del tramo sobre el que se aplica. Esta fuerza se considera que actúa en el centro del tramo.

Ejemplo con Empotramiento y Carga Repartida

Imagina una viga empotrada en un extremo y con una carga repartida uniforme a lo largo de su longitud. Para calcular las reacciones en el empotramiento, podemos convertir la carga repartida uniforme en una fuerza concentrada equivalente.

En este caso, la fuerza concentrada equivalente sería la carga repartida uniforme multiplicada por la longitud de la viga. Esta fuerza se considera que actúa en el centro de la viga.

Para calcular las reacciones, podemos aplicar la ecuación de equilibrio de momentos alrededor del empotramiento.

Tipos de Estructuras: Guía Completa de Cargas, Esfuerzos y Tecnología

• La fuerza concentrada equivalente genera un momento negativo porque genera un giro en sentido de las agujas del reloj.
• La reacción vertical en el empotramiento genera un momento positivo porque genera un giro en sentido contrario a las agujas del reloj.
• La reacción horizontal en el empotramiento no genera momento porque su línea de acción pasa por el punto de referencia.

Resolviendo la ecuación de equilibrio de momentos, obtenemos las reacciones en el empotramiento.

Métodos de Cálculo

Método de la Integral de Área

Además de las ecuaciones de equilibrio, existe otro método para calcular los diagramas de esfuerzos cortantes y momentos flectores: el método de la integral de área.

El método de la integral de área se basa en el concepto de que la integral del diagrama de esfuerzos cortantes es igual al diagrama de momentos flectores.

Para utilizar este método, se debe integrar el diagrama de esfuerzos cortantes a lo largo de la viga. El resultado de la integración es el diagrama de momentos flectores.

Comparación con Ecuaciones de Equilibrio

El método de la integral de área y los métodos de las ecuaciones de equilibrio son equivalentes en cuanto a los resultados que se obtienen.

El método de la integral de área es especialmente útil cuando se tienen cargas distribuidas, ya que simplifica el cálculo del diagrama de momentos flectores.

Convención de Signos

Momentos y Fuerzas

Para asegurar la consistencia en los cálculos, es importante utilizar una convención de signos definida para los momentos y las fuerzas.

Una convención de signos común es la siguiente:

• Momentos: Los momentos que generan un giro en sentido contrario a las agujas del reloj se consideran positivos. Los momentos que generan un giro en sentido de las agujas del reloj se consideran negativos.
• Fuerzas: Las fuerzas que actúan hacia arriba se consideran positivas. Las fuerzas que actúan hacia abajo se consideran negativas.

Importancia de la Consistencia

La utilización de una convención de signos consistente en todo el cálculo es fundamental para obtener resultados correctos.

Si se utilizan diferentes convenciones de signos para diferentes elementos del cálculo, se pueden obtener resultados erróneos.

Resistencia de Materiales: Conceptos Básicos y Aplicaciones Prácticas

Es importante recordar que la convención de signos es una cuestión de acuerdo, y se puede utilizar cualquier convención siempre y cuando se mantenga consistente en todo el cálculo.

el cálculo de reacciones en vigas y la construcción de diagramas de esfuerzos y momentos son procesos fundamentales en la ingeniería estructural. La comprensión de la sumatoria de momentos y las ecuaciones de equilibrio, junto con la correcta utilización de una convención de signos, son esenciales para obtener resultados precisos y fiables.

Video sobre Cálculo de Vigas Fácil: Sumatoria de Momentos y Diagramas de Esfuerzos

Preguntas Frecuentes

¿Qué es la sumatoria de momentos y cómo se relaciona con el equilibrio de una viga?

La sumatoria de momentos, también conocida como sumatorio de momentos, es un concepto fundamental en la mecánica de sólidos, particularmente en el análisis de vigas. Es la suma algebraica de los momentos de todas las fuerzas que actúan sobre un cuerpo rígido. En otras palabras, es la suma de las fuerzas multiplicadas por sus distancias al punto de referencia. Para que una viga esté en equilibrio estático, la sumatoria de momentos alrededor de cualquier punto debe ser igual a cero. Esto significa que las fuerzas que tienden a hacer girar la viga en un sentido deben ser compensadas por las fuerzas que tienden a hacerla girar en sentido contrario.

La sumatoria de momentos juega un papel crucial en el cálculo de reacciones en los apoyos de una viga. Al aplicar la ecuación de equilibrio de momentos, podemos determinar las fuerzas que se generan en los apoyos para contrarrestar las cargas externas que actúan sobre la viga. Esta ecuación es una herramienta fundamental para garantizar la estabilidad y el correcto comportamiento de la estructura.

¿Cómo se determina el signo del momento en la sumatoria de momentos?

El signo del momento depende de la dirección del giro que produce la fuerza. Si el giro es en sentido contrario a las agujas del reloj, el momento es positivo. Si el giro es en sentido de las agujas del reloj, el momento es negativo.

Una forma práctica de recordar esto es imaginar que estás mirando la viga desde un punto de vista perpendicular a su plano. Si la fuerza tiende a hacer girar la viga hacia arriba, el momento es positivo. Si la fuerza tiende a hacer girar la viga hacia abajo, el momento es negativo.

La consistencia en la aplicación de esta convención de signos es fundamental para obtener resultados correctos. Si se utiliza una convención de signos inconsistente, se obtendrán resultados erróneos.

¿Cómo se calcula la fuerza concentrada equivalente para una carga repartida uniforme?

Cuando se tiene una carga repartida uniforme sobre un tramo de una viga, es útil convertirla en una fuerza concentrada equivalente para simplificar los cálculos. Esta fuerza concentrada equivalente se obtiene multiplicando la carga repartida uniforme por la longitud del tramo sobre el que se aplica. La fuerza se considera que actúa en el centro del tramo.

Por ejemplo, si una carga repartida uniforme de 10 kN/m se aplica sobre un tramo de 2 metros de longitud, la fuerza concentrada equivalente sería de 20 kN (10 kN/m * 2 m).

La conversión a fuerza concentrada equivalente facilita el cálculo de reacciones y diagramas de esfuerzos y momentos, especialmente en casos con cargas distribuidas.

¿Cuál es la diferencia entre el método de la integral de área y las ecuaciones de equilibrio para calcular diagramas de esfuerzos y momentos?

El método de la integral de área y las ecuaciones de equilibrio son dos métodos equivalentes para calcular diagramas de esfuerzos cortantes y momentos flectores.

Las ecuaciones de equilibrio se basan en las leyes de Newton para la estática, mientras que el método de la integral de área se basa en la relación entre el diagrama de esfuerzos cortantes y el diagrama de momentos flectores. la integral del diagrama de esfuerzos cortantes es igual al diagrama de momentos flectores.

El método de la integral de área es particularmente útil cuando se tienen cargas distribuidas, ya que simplifica el cálculo del diagrama de momentos flectores. Sin embargo, ambos métodos son válidos y proporcionan resultados equivalentes.

¿Qué es una convención de signos y por qué es importante?

Una convención de signos es un conjunto de reglas para determinar el signo de las fuerzas, momentos y otras magnitudes en un problema de estática. Es importante utilizar una convención de signos consistente en todo el cálculo para obtener resultados correctos.

Si se utilizan diferentes convenciones de signos para diferentes elementos del cálculo, se pueden obtener resultados erróneos. Por ejemplo, si se considera que un momento que gira en sentido contrario a las agujas del reloj es positivo y luego se utiliza la convención opuesta para otro momento en el mismo problema, el resultado final será incorrecto.

Las convenciones de signos comunes en la mecánica de sólidos incluyen:

• Momentos: Los momentos que generan un giro en sentido contrario a las agujas del reloj se consideran positivos, mientras que los que generan un giro en sentido de las agujas del reloj se consideran negativos.
• Fuerzas: Las fuerzas que actúan hacia arriba se consideran positivas, mientras que las que actúan hacia abajo se consideran negativas.

Es importante elegir una convención de signos y mantenerla consistente durante todo el cálculo para garantizar la precisión de los resultados.

A Modo de conclusión

Dominar el cálculo de reacciones en vigas es crucial para cualquier ingeniero estructural. Mediante la sumatoria de momentos y el análisis de diagramas de esfuerzos, podemos comprender la distribución de fuerzas y momentos a lo largo de la viga, determinando las reacciones en los apoyos y la resistencia interna de la estructura. El método de la integral de área nos ofrece un camino alternativo para obtener los diagramas de esfuerzos y momentos, siendo especialmente útil en casos de carga distribuida. La consistencia en la aplicación de la convención de signos es fundamental para obtener resultados precisos y evitar errores en los cálculos.

Compartelo

¡Aprende a calcular vigas como un profesional! ️ Este artículo te ayudará a comprender los conceptos básicos del cálculo de vigas, desde la sumatoria de momentos hasta la creación de diagramas de esfuerzos. Descifra las reacciones en los apoyos, las fuerzas internas y los momentos flectores. ¡Comparte este conocimiento con tus amigos y colegas para construir estructuras más seguras y eficientes! #CálculoDeVigas #IngenieríaCivil #Estructuras #MomentosFlectors #DiagramasDeEsfuerzos